>>187747
>среди любых n+1 чисел
Т.е. например n = 2, тогда имеем {1, 2, 3, 4}. Тогда в подмножествах {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4} (сочетания из 2n по n+1) всегда будут такие числа a и b, что а кратно b.
>>187741
1. Этот боян даже у Гарднера встречается. 2 кг (точнее, ~20 Н). При условии наличия силы тяжести, трактовки слова "полкирпича" как "полкирпича по массе" и прочих очевидных условий, принимаемых в таких задачах по дефолту, если не оговорено противное (во избежание ебланской софистики).
2. По индукции, например. Для n=1 (т.е. для пары {1,2}) утв. тривиально. Пусть оно справедливо для некого произвольного n. Докажем, что тогда оно справедливо для n+1, т.е. что для последовательности чисел {1,2,..., 2(n+1)} выборка любых n+2 чисел содержит пару кратных чисел.
Рассм. эту последовательность как {1,2,..., 2n, 2n+1, 2n+2}={A,B}, где обозначено подмн-во A={1,2,..., 2n} и подмн-во B={2n+1, 2n+2}. Имеются три случая.
а) выборка N из n+2 шт. чисел целиком лежит в A. Тогда, т.к. n+2>n+1, срабатывает индуктивное предположение для случая n+1 чисел внутри A={1,...,2n} => искомая кратная пара найдется в А, ч.т.д.
б) n+1 чисел из выборки N лежат в A, одно число в B. Опять срабатывает индуктивное предположение внутри A аналогично предыдущ. случаю.
в) Ровно n чисел из выборки N лежит в A, остальные 2 числа [равные тогда в точности 2n+1 и 2(n+1)] -- в B. Если среди n чисел в А есть пара кратных -- искомая пара существует, ч.т.д. Поэтому предположим противное: среди n чисел в А нет пары кратных. Пусть среди этих n чисел присутствует число, равное n+1. Тогда ему кратно последнее число из мн-ва B, равное 2(n+1) => искомая пара кратных существует, ч.т.д. Поэтому предположим оставшийся случай, что среди n чисел в А нет числа n+1. Заметим, что если бы мы его мысленно добавили к этим n числам из А, то мы получили бы (n+1) шт. чисел в A, среди которых тут же нашлась бы пара кратных (по индуктивному предположению). А раз без такого добавления пара кратных по нашему текущему предположению не возникает, то это означает, что пара кратных образовалась бы в точности из числа n+1 и еще какого-то числа a внутри А. Значит, в нашей выборке n чисел из А существует некое число а такое, что ka=n+1, где k>1 -- натуральное. Другой возможный случай кратности -- k(n+1)=a -- невозможен, т.к. тогда а было бы не меньше 2(n+1), выходя за пределы А. Но это значит, что число из мн-ва B, равное 2(n+1) (и входящее в выборку N из n+2 чисел по предположению п. в), автоматически кратно числу а с коэффициентом 2k, а именно, 2ka=2(n+1). Таким образом, искомая кратная пара построена и для этого случая. Ч.т.д.
>>187767
Молодец, вроде всё верно. Ты студент-математематик или как?
Вот ещё:
3. Можно ли соединить все вершины куба шестизвенной замкнутой ломаной?
4. Вершины куба пометили числами от 1 до 8. Для каждого ребра нашли произведение номеров соответствующих вершин. Полученные числа сложили. Найти наибольшее возможное значение суммы.
5. Можно ли найти площадь кольца (из круга удален концентричный ему круг), произведя всего одно линейное измерение?
>>187786
5. Площадь кольца равна разности площадей кругов радиусами R и r, то есть pi(R2 - r2). Нужно измерить второй катет прямоугольного треугольника с катетом r и гипотенузой R.
>>187786
>Ты студент-математематик или как?
Я закончил вуз уже. Физик.
>>187786
Из каждой вершины должно выходить минимум по два ребра ломаной. Ребро соединяет две вершины. У куба 8 вершин, чтобы их соединить, понадобится 8 рёбер.
>>187767
>точнее, ~20 Н). При условии наличия силы тяжести, трактовки слова "полкирпича" как "полкирпича по массе" и прочих очевидных условий, принимаемых в таких задачах по дефолту, если не оговорено противное (во избежание ебланской софистики).
Лолблядь. Хотел избежать софистики и сам же ее развел. Только конченый дебил будет в математической задачке искать закавыку физического смысла.
>>187808
Нормальное замечание. Вес - это вес, а масса - это масса. Пишите точно.
>>187808
>Хотел избежать софистики и сам же ее развел.
No.
>Только конченый дебил будет в математической задачке искать закавыку физического смысла.
Никаких закавык тут не искалось, а напротив, были сделаны превентивные меры против того, чтобы ебланы наподобие тебя не пришли и не начали эти закавыки искать, разводя нерелевантную хуйню. Хотя не помогло.
>>187802
>Из каждой вершины должно выходить минимум по два ребра ломаной
Это неверно. Во-первых, что такое "ребро ломаной"? Во-вторых, ты, видимо, решаешь задачу только на поверхности куба, а в условии об этом не говорилось. Т.е. ломаные могут быть вне куба, внутри него или на его поверхности.
>>187815
>Пусть есть множество из n+1 элементов, содержащее 2n и 2n-1. Почему в нём есть неравные кратные элементы?
По изначальному предположению: пусть утверждение доказано для n, т.е. любое сочетание по n+1 элементов из множества {1, 2, ..., 2n} содержит такие a и b, что a кратно b.
>Нужно явно оговорить, что a!=b, иначе задача тривиальна.
Ну это уже мелочи, нашёл к чему придираться.
>>187815
>Пусть есть множество из n+1 элементов, содержащее 2n и 2n-1. Почему в нём есть неравные кратные элементы?
Если это множество лежит в пределах {1,.., 2n}, то док-во наличия кратных элементов -- это как раз исходная задача и есть. А если оно какими-то своими элементами вылазит за пределы {1,.., 2n}, тогда никаких гарантий, что в нем будут кратные элементы, нет. А к чему этот вопрос?
>>187823
>Это неверно.
есть граф
a-1-b-2-с-3-d-4-e-5-f-6-g-7-h-8-a
буквы - вершины ака вершины куба, цифры - рёбра ака звенья ломаной. Если вершина инцидентна только одному ребру, то она является концом ломаной, а в замкнутой ломаной нет концов. Если среди рёбер 1, 2, ... , 8 есть одинаковые, то одно ребро соединяет более чем две вершины, чего быть не может.
>>187825
В этой задаче вершина инцидентна ломаной тогда и только тогда, когда она принадлежит отрезку ломаной. Например, на рисунке изображена трехзвенная незамкнутая ломаная, которая "соединяет" четыре вершины. Надеюсь, теперь условия понятны.
>>187825
Слишком просто. Например, можно придумать случай, когда 8 точек на плоскости соединены 4-звенной ломаной (пикрелейтед). Так что если пытаться доказывать невозможность этого в случае куба, то нужно использовать характер их пространственного расположения (никакие 3 не лежат на прямой и никакие 5 не лежат в одной плоскости, например).
 [url]
[url]Анонимы, был в треде у программистов - ничего не подсказали. Думаю\надеюсь, что здесь помогут.
Нужна годная годная литература по алгоритмам и околоалгоритмам : Теория игр, Дискретная математика, теория алгоритмов и т.д (можно наверное это совместить в понятии "прикладная математика").
Какие-то книги нашёл, какие-то ищу. Но Проблема в том что ,например, большинство книг по теории игОр, из тех, что я видел написаны не позже 80-90 годов. А совсем новые книги тоже как то сразу доверия не вызывают.
>>187939
Кнут "Искусство программирования", Гранам-Кнут "Конкретная математика", Кормен-Лейзерстон-Ривест-Штайн "Алгоритмы: построение и анализ".
>>187955
Пожалуйста. Если ты новичок пока, то из этих трёх советую начать с "Конкретной математики". "Искусство программирования" -- многотомный и тяжелый труд, "Алгоритмы" тоже непросто читать.
Ещё знаю две книжки: "Дискретная математика для программистов" Новикова и книга с таким же названием Хаггарти. Ни одну из них я не читал, но вроде считаются классическими в этой области.
Есть две пачки сушеных бананов по 1 кг каждая. Сорта бананов разные: в первой пачке пищевая ценность бананов такова, что 1 кг этих бананов = 7 кг обычных бананов (иными словами, от 1 кг этих бананов наешься так же, как от 7 кг обычных), а во второй пачке 1 банан = 7 обычным бананам. Какую пачку вы купите, если стоят они одинаково, а вы очень голодны?
Решаема ли данная задача? Если нет, то почему?
Здравия желаю,анон.Поясни про "Бесконечность множества простых чисел",а точнее про доказательство от Евклида:Представим, что количество простых чисел конечно. Перемножим их и прибавим единицу. Полученное число не делится ни на одно из конечного набора простых чисел, потому что остаток от деления на любое из них даёт единицу. Значит, число должно делиться на некоторое простое число, не включённое в этот набор. Противоречие..
Я пробую построить один из рядов с границей 13,т.е.2*3*5*7*11*13+1=30031,но ответ не является простым числом(59*509=30031).Почему оно составное?
>>187963
>Почему оно составное?
Оно и не обязано быть простым. Но оно не делится на 2,3,5,7,11,13, а делится на большее простое число (на 59, напр.). Либо само могло бы быть простым, тогда оно было бы заведомо больше 13. Значит, в любом случае 13 - не последнее простое число, чтоитребовалось проиллюстрировать.
>>187964
Спасибо.Я только сейчас осознал,что плохо прочитал теорему.Добра.
>3. Можно ли соединить все вершины куба шестизвенной замкнутой ломаной?
>4. Вершины куба пометили числами от 1 до 8. Для каждого ребра нашли произведение номеров соответствующих вершин. Полученные числа сложили. Найти наибольшее возможное значение суммы.
Итак, если анон не решит до сегодняшнего вечера, то я запощу решения.
Наукач, помоги решить задачку.
Есть последовательность: x(i+1) = x(i)/2, если x(i) - четное, или x(i+1) = 3*x(i) + 1, если нечетное. x(0) = n, некое натурально число. Надо доказать, что в этой последовательности для любого n рано или поздно встретится единица.
>>187977
Иди нахуй, еблан со своей гипотезой Коллатца. Думаешь, тут одни ламаки собрались?
>>187977
Нужно доказать, что рано или поздно встретится степень двойки, т.к. они и только они ведут к 1 всегда.
>>187741
>>196073
Хиккач, поясни по хардкору за нахождение мам методом Крылова. В матрице -4 4 2/-1 1 1/-5 4 3 n-вектор последовательности не выражается как линейная комбинация предыдущих. Алсо, реквестирую какой-нибудь годный способ.
>>187968
>3. Можно ли соединить все вершины куба шестизвенной замкнутой ломаной?
Да, см. рис. 1.
>4. Вершины куба пометили числами от 1 до 8. Для каждого ребра нашли произведение номеров соответствующих вершин. Полученные числа сложили. Найти наибольшее возможное значение суммы.
264. См. рис. 2 и 3 (мне кажется, удобнее рассматривать планарный граф, поэтому добавил рис. 3).
Новые задачи:
5.1. Расставить по кругу натуральные числа от 1 до 21 так, чтобы соседние числа отличались либо на 4, либо на 9.
5.2. Доказать, что существует такое натуральное n, что для любого N > n, можно расставить по кругу натуральные числа так, чтобы соседние числа отличались либо на 4, либо на 9.
>>187961
Спасибо,Бро
Помогите разобраться с определением тригонометрических функций с вещественными/комплексными аргументами. Зачем оно вообще надо, почему не хватает значений углов в радианах как аргументов?
>>187741
1. Почему вы пишите что он весит 2 килограмма? Сказано, что он весит килограмм, а так как после слова "килограмм" нет запятой то вторая часть задачи не имеет смысла, это как если был задан вопрос: "на улице сейчас идет дождь а дома у меня есть коричневый диван. Какая сейчас погода?".
>>188206
Лолшто? Тут нет никакой "второй части задачи". m = 1 + m/2, если m -- масса кирпича. Что тут может быть непонятного?
>>188199
>Помогите разобраться с определением тригонометрических функций
Это такой бесконечный ряд, полином.
Q: Какая разница, что за аргумент в этом полиноме?
A: Это дает ряду некоторые интересные свойства. Тригонометрические функции могут быть от комплексных чисел, от векторов, матриц, от чего угодно можно определить, если постараться.
>>188214
> Это такой бесконечный ряд,
> полином.
> бесконечный ряд
Поссал на дебила.
>>188034
>5.1. Расставить по кругу натуральные числа от 1 до 21 так, чтобы соседние числа отличались либо на 4, либо на 9.
9 18 14 5 1 10 19 15 6 2 11 20 16 7 3 12 21 17 8 4 13
>>188225
Да.
Подсказка ко второй части задачи: "расставление по кругу" -- это поиск гамильтонова цикла в графе с вершинами {1..21} и ребрами "длиной" 4 и 9. Эти циклы из графов с одинаковыми ребрами можно "склеивать", получая большие циклы из меньших.
>>188250
Идеи по цикличной "склейке" есть. Сложности с "краевыми" эффектами
Суп, анон, я тупой и читаю "Основания математики" Гильберта. Только начал и уже непонятно (см. пикрелейтед) - если бы не было комментария, то как бы я догадался, что Gr - это прямая? (судя по тому, что написано выше, это "некоторые отношения между x и y). Почему там два икса?
>>188280
Об этом ничего не говорится, сходу начитается вот эта поеботня. Я уже решил дропнуть, не для меня явно эта книга.
Gr - это 3-х местное отношение. Три точки p, q, t находятся в отношении Gr(p, q, t) если они лежат на одной прямой.
Для двух точек x, y отношение записывается Gr(x, x, y). Здесь p это x, q это x, t это y.
>>188278
А ты и не должен был догадываться, что Gr - это прямая. В этом вся суть метода Гильберта. Смотри на буковки, не ищи в них смысла ёпт.
>>188286
Ну, то есть даны аксиомы A1 и A2, то ты должен медитировать над выводом из них теорем по строгим формальным правилам, и совершенно неважно, из какой математической теории эти аксиомы были выдраны и какой смысл в них изначально вкладывался. И вопрос об их осмысленности тоже не ставится.
Гильберт сгенерировал последовательность буковок, удовлетворяющую определённым правилам. Смысла в ней не ищи, поскольку смысл в неё не вкладывался.
>>188286
Вкладывался. Это абстрагирование при помощи логики предикатов. Помимо формального вывода необходимо чтобы он был адекватен (sound), какой-либо интерпретации (например Евклидовой геометрии).
>>188290
Пример. Дана формальная теория с modus ponens.
Аксиомы:
A1. P(t) -> P(tt) # t - метаматематическая буква
A2. P(a)
Вывод.
P(a) # аксиома A2
P(a) -> P(aa) # аксиома A1
P(aa) # modus ponens
P(aa) -> P(aaa) # аксиома A1
P(aaa) # modus ponens
P(aaa) -> P(aaaa) # аксиома A1
P(aaaa) # modus ponens
Совершенно не важно, могут ли буквы выше означать хоть что-то. Важно выводить строки буковок по определённым правилам. Смысл изгнан.
>>188291
Нет, не вкладывался. Гильберт не требует существования какой бы то ни было интерпретации.
>>188296
Именно. Смысла нет, геометрическая интуиция запрещена, осознание запрещено. Есть бессмысленные буквы, и есть правила. Пиши строки букв и не ставь вопрос о смысле. Так выглядит математика по Гильберту, написание бессмысленных строк букв.
>>188299
Ты утрируешь.
>геометрическая интуиция запрещена, осознание, запрещено.
>запрещено
Пруф. Хотя бы из того же "foundations of mathematics"
Есть бессмысленные буквы, и есть правила. Пиши строки букв и не ставь вопрос о смысле.
Собачий бред.
Так выглядит математика по Гильберту, написание бессмысленных строк букв.
>Полный собачий бред.
Еще раз: "математика по-Гильберту" это введение строгой аксиоматики. Это инструмент, который весьма удобен, изящен и надежен. Для чего ты его применять собираешься - твое дело. Из жонглирований буковками более-менее осмысленной и мм... "плодотворной" теоремы не выведешь (in feasible time). Не мели ерунды.
>>188282
Gr=Gerade=прямая. О предикате Gr(x,y,z) можно думать как о "x,y,z лежат на одной прямой".
Zw=Zwischen=между. О Zw(x,y,z) можно думать как "x лежит между y и z".
>>188301
>Полный собачий бред.
Разрыв шаблона детектед. Добро пожаловать в клуб игроков в бисер.
>Из жонглирований буковками более-менее осмысленной и мм... "плодотворной" теоремы не выведешь
Это осознаёшь ты, но этого не осознавал ни Гильберт, ни его генералистые последователи.
>Ты утрируешь.
Я знаком с работами метаматематиков. Они видели математику именно так, как я описал.
>>188304
Кто первым связал синтаксис с семантикой? Гедель?
Спасибо, анон, не думал, что ответишь. Я вообще искал книгу, с помощью которой можно перепрыгнуть через аристотелеву логику - читаю сейчас "Историю западной философии" Рассела, он там говорит, что человечество на 2000 лет застряло на Аристотеле, а я даже не понимаю в чем был прорыв в 19ом веке.
>>188315
Никакого прорыва. Как сидели на Аристотеле, так и сидим. Все остальное - те или иные надстройки сводимые к старому доброму M.P. и аксиомам.
...Лотфи-Заде правда попытался рыпнуться, но в основном в сторону семантики. Ну Колмогоров еще с зоопарком логик. Но это все... Чехлы.
Ну можно конечно свои правила зафигачить, но мышление по которым эти правила строиться будут - Аристотелево. Нда, это уже метаметаматематика получается.
Вот так. Пожинаем, то что посеяли.
>>188315
Открытие исчисления предикатов Г. Фреге. По существу от этого идёт вся современная логика.
Стороны прямоугольника заданы натуральными числами M и N. Составить программу, которая будет находить, на сколько квадратов, стороны которых выражены натуральными числами, можно разрезать данный прямоугольник, если от него каждый раз отрезается квадрат максимально большой площади.
Другими словами: какова сложность алгоритма Евклида вычитанием?
Почему бы вам просто не проследовать в направлении project euler?
>>188930
Там вы найдете гораздо больше подобных задач, в широком диапазоне сложности.
>>188293
>P(aa) -> P(aaa) # аксиома A1
Поздравляю, вы официально приглашаетесь на специальную олимпиаду 2015 в Лос-Анжелес. Приглашение получите по почте.
Надо же так обосраться в собственном примере.
Ln(i)=i*pi/2
Какого хуя? Может кто находчиво объяснить?
>>188958
2*Ln(i) = i*pi
2*Ln(i) = Ln(-1) (по тождеству Эйлера)
2*Ln(i) = Ln(i^2)
2*Ln(i) = 2*Ln(i) (т.к. Ln(x^2) = 2*Ln(x))
>>188983
Спасибо, я упускал тождество Эйлера.
Также, сам доказал так:
i=cos(pi/2)+i*sin(pi/2), значит fi=pi/2, p=1;
т.к cos(fi)+i*sin(fi)=e^i*fi, то cos(pi/2)+i*sin(pi/2)=e^i*(pi/2)
i=e^i*(pi/2);
ln(i)=ln(e^i*(pi/2))=i*(pi/2)
>>188995
Интересно, А Мишаня Верб. с Ромчиком Мих. на двачи захаживают?
>>189110
А чем тебе интересен последний? (Роман Михайлов же?)
>>189110
Ньюфаг детектед. Миша ещё тот самый обсирал, причём взаимно.
Детский вопрос. Как посчитать площадь параллельной проекции эллипсоида на произвольную плоскость?
Доказать, что уравнение x^3 + y^4 + z^5 + u^6 + v^7 + w^8 = t^9 имеет бесконечно много решений в натуральных числах.
>>190051
принимаем левую часть равную M, получаем М = t^9, тривиально
гуманитарий, так что мож чего не понял
>>190054
забыл что такое натуральные числа, прикинь!
прошу простить убогого
- Циркулярная дефиниция. Вопрос инвалид.
2. Матиндукция, писать было лень, попробовал устно, но ниасилил. Письменно только опущенки такую хуиту решают.
Есть два стула: "Основания математики" Гильберта и "Основания математики" Рассела. Кто-нибудь читал оба многотомника? Дайте сравнительную оценку.
Ландсберг или Пёрышкин?
>>190174
Это ответ. Оба талмуда неинтересны никому, кроме историков математики, отражают провалившиеся концепции и написаны, исходя из состояния науки на конец XIX века. Поэтому что то хуйня, что это хуйня.
А кто-нибудь тут читал "Что такое математика?" Курант/Роббинс? Я сейчас в процессе чтения и нахожу книгу очень годной, а отзывов о ней маловато в интернетах.
>>190191
Читал, годнота. Лучей добра тебе, удачно дочитать.
>>190194
Просто не прочитав эти книги можно разбираться в математике на приличном уровне. Но в истории математики и вкладе философии в ее развитие эти книги имеют ключевое значение.
>>190211
Вопрос здесь в том, начнешь ли разбираться в математике на приличном уровне после прочтения этих книжек.
Эй, матанщики и матанята, а что такое дифференциал?
>>190219
1. Скорость изменения функции.
2. Касательная к графику функции.
>>188034
>264
Только вкатился. А как доказать, что оно максимальное?
>>190219
Дифференциалом функции f в точке x называется линейная функция d такая, что для любой точки a верно, что d(a) = f(x + a) - f(a) + o(a), где o - бесконечно-малая в точке x функция. То есть имеется фиксированная точка x, для любой другой точки вычисляется разность значений функции f в этих точках, и эта разность должна быть почти равна дифференциалу.
Профиты дифференцирования в том, что произвольная функция приближается некоей линейной функцией.
>>190219
>что такое дифференциал?
Смотря какой (а то мало ли, мож ты тролль и тебе, блять, автомобильный подавай). Первый дифференциал ф-ции одной переменной -- линейная (по приращению аргумента) часть приращения функции, если таковая существует. Т.е. если у тебя ф-ция f(x) при приращении агрумента на Δx приобретает приращение Δf=f(x+Δx)-f(x), представимое в виде Δf=a(x)Δx+o(Δx), тогда главную линейную по Δx часть этого приращения df=a(x)Δx и называют дифференциалом ф-ции f в данной точке x. Можно показать, что ф-ция a(x) при этом оказывается равна производной f'(x). Так что дифференциал может быть записан в виде df(x)≡f'(x)Δx. Иногда это даже берут в качестве исходного определения дифференциала. Применяя данную формулу к функции f(x)=x, где x - независимая переменная, получим dx=Δx, так что дифференциал независимой переменной dx и ее приращение Δx суть одно и то же. В результате получаем хорошо знакомую всем формулу для дифференциала: df(x)≡f'(x)dx, чем обосновывается известное обозначение для производной f'(x)≡df(x)/dx.
Первый дифференциал ф-ции многих аргументов -- это тоже линейная (по каждому приращению каждого аргумента) часть приращения ф-ции. И ее можно свести к формуле df(x1,...,xn)=∂f/∂x1dx1+...+∂f/∂xndxn=Σ∂f/∂xidxi≡∇f(x)⋅dx (все частные производные берутся в данной точке x=(x1,...,xn))
Как обычно, в тред влезает троллота
со своими выебонами >>190326 про дифференциал 1-форму градиента ф-ции f(x) на мноогобразии, обозначаемую df и определяемую своим действием на произвольное векторное поле v по правилу df(v)=v(f)≡vi∂f/∂xi, где вектор v понимается как дифференциальный оператор на пространстве скалярных ф-ций. Применяя это правило поочередно к ф-циям f(x)=xi (i=1...n) при действии на базисные векторы ek, легко получить, что dxi(ek)=δik, в силу чего 1-формы dxi образуют дуальный базис, и 1-форма градиента df раскладывается по ним в виде df=∂f/∂xidxi, что напоминает классическую запись дифференциала, хотя отождествлять 1-форму с классическим пониманием дифференциалом некорректно, т.к. в классическом смысле дифференциал есть скаляр (главная линейная часть приращения ф-ции): df=∇f(x)⋅Δx (см. выше).
Линейным оператором f является отображение из A в B, где A и B - линейные пространства.
Сопряжённым оператором к f является отображение f' из B' в A', где A' и B' - множества линейных функционалов на A и B.
Оператор называется самосопряжённым, если он совпадает со своим сопряжённым.
То есть f = f'. Это возможно, только если A является B', а B является A'.
Рассмотрим оператор id, который часто приводят в качестве примера самосопряжённого оператора. Тогда A=B и A' = B = A. То есть множество всех линейных функционалов на A есть само A. Я не могу это осознать. Как же так?
>>190354
> Для выбранной локальной карты x_1,\;\ldots,\;x_n, дифференциалы d_px_i представляют собой базис кокасательного простанства
И ты идёшь на хуй.
>>190384
Это не дифференциалы в классич. матанском понимании, а 1-формы, блеать. Если копипастишь Википедию, то ориентируйся в контексте. Которые таки да, иногда называют "дифференциалами" (когда сам дифференциал определяют как линейное отображение). Вопрос терминологии.
 [url]
[url]Видеорилейтед. Вторая сумма (S2) умножается на два, вторая часть этой суммы сдвигается вправо. Раз она сдвигается вправо, где теряется ее последний член?
>>190401
Нигде он не теряется. Смотри статью в Вики, если что-то не понял (http://ru.wikipedia.org/wiki/1_%2B_2_%2B_3_%2B_4_%2B_%E2%8B%AF)
Вообще исходные ряды, которые применялись в доказательстве, расходятся, поэтому не имеют суммы в принципе (как и 1+2+3+...). Но если применить некоторые особенные методы (суммирования не в классическом понимании), то получается -1/12.
>>187741
ебанутые задачки на смекалку, благо, русский язык позволяет изъёбываться как угодно.
>>190182
>Оба талмуда неинтересны никому, кроме историков математики, отражают провалившиеся концепции и написаны, исходя из состояния науки на конец XIX века
Что же тогда из популярного отражает состояние мат. логики современности?
Не могу понять стереографическую проекцию сферы на плоскость, может кто поможет? http://ru.wikipedia.org/wiki/%D0%A1%D1%82%D0%B5%D1%80%D0%B5%D0%BE%D0%B3%D1%80%D0%B0%D1%84%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B0%D1%8F_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%86%D0%B8%D1%8F
>>190358
Если я ничо не путаю, самосопряженность вводится для операторов в евклидовых, гильбертовых и пр. пространствах, где определено скалярное произведение. Тогда каждый вектор такого пр-ва можно рассматривать как лин. функционал на всех векторах этого же пр-ва, действующий на них скалярным умножением, например. Вот и получается, что само пр-во можно рассматривать как дуальное над самим собою же.
>>190437
Сфера - это поверхность шара, можно воображать её как пустой внутри шар.
Ставим сферу на плоскость. Из точки, противоположной точке касания, испускаем бесконечно много прямых. Каждая прямая пересечёт сначала сферу в одной точке, а потом плоскость в одной точке. Таким образом получится отображение точек сферы на плоскость. Отобразятся все точки, кроме точки, из которой испущены прямые.
>>190458
Всё понятно, спасибо! Ушёл писать программу для 3Д сферы.
>>190406
Да ну, хуйня какая-то (я не >>190401). Нельзя так с рядами расходящимися. Так же можно любую хуйню обосновать, вот например:
Возьмем S = 1+2+3+4+5+...
Рассмотрим S-S, но вычитать будем со смещением (как в видео он складывает S2+S2), получим:
S-S = 1+(2-1)+(3-2)+(4-3)+... = 1+1+1+1+1+...
То есть мы пришли к тому что 1+1+1+1+1+... = 0
Окей, положим это не хуйня собачья (хотя уже здесь видно, что хуйня) и умножим обе стороны равенства на 2:
2+2+2+2+2+... = 0
Ну охуенно, чо.
А теперь давайте снова посчитаем S-S, но теперь уже со смещением в два члена:
S-S = 1+2+(3-1)+(4-2)+(5-3)+(6-4)+... = 1+2+2+2+2+2+2+...=0
Из последнего получается, что 2+2+2+2+2+2+...= -1
Но мы выше пришли к тому, что 2+2+2+2+2+2+...= 0
Мы пришли к противоречию (или к тому, что 0 = -1 ШОК СЕНСАЦИЯ), а значит творить подобную хуиту с рядми нельзя. ЧТД.
Анонасы, что то в гугле не нашёл решения. Помогите пожалуйста. Ещё одну задачу добить и закрою зачёт.
Для работы на N ПЭВМ случайным образом распределяются K студентов. Под состоянием совокупности из N ПЭВМ будем понимать вектор k = (k1, k2, ..., kN), где ki — число студентов, которые выполняют своё задание на i-й ПЭВМ, sumi = 1, N(ki) = K. Состояния считаются различными, если им соответствуют вектора с различными компонентами. Найти: а) число состояний сети, б) вероятности состояний, предполагая, что все состояния равновозможные.
>>190191
Ну вот решил я глянуть про что там пишут, открыл на первом попавшемся месте и у меня сразу вопрос. Вот они пишут
>2. Десятичные дроби: конечные и бесконечные.
>Чтобы покрыть числовую ось везде плотным множеством точек, нет необходимости использовать всю совокупность рациональных чисел: достаточно, например, ограничиться только теми числами, которые возникают при подразделении единичного отрезка на 10, потом на 100, 1000 и т.д. равных частей. Получающиеся при этом точки деления соответствуют «десятичным дробям».
И как это понимать? Что значит "достаточно ограничиться"? Я же все равно буду вынeжден бесконечно продолжать это "и т.д.", если действительно захочу покрыть числовую ось везде плотным множеством точек. Так в чем тут ограничение?
>>190609
Нужно просто придумать более общее понятие сходимости, нежели предел частичных сумм. Тогда и с расходящимися в обычном смысле рядами можно будет работать, но далеко не на таком пальцевом уровне как у тебя или в том видео.
>>190655
Наверно, тут имеется в виду, что не обязательно брать все возможные знаменатели, а ограничиться степенями 10. В то же время числа все будут те же, а представить их мы можем в неком особенном общем виде со знаменателями одного типа.
А вот мне интересно: есть в этом треде профессиональные математики? Преподаватели там или молодые учёные, ну или хотя бы бывшие студенты, работающие именно в математическом направлении?
>>190191
на самом деле это классика, в своём роде
примерно как "история западной философии" б. рассела
>>190219
по-моему, все данные ответы - это невообразимая хуйня, понаписанная школотой
на самом деле, дифференциал функции (в точке) - это линейное отображение между касательными пространствами.
например, дифференциал функции f: R^n -> R^m представлен её матрицей Якоби. и правда, линейные отображения представляются в виде матрицы, например
>>190675
судя по тому, что здесь пишут о дифференциале, - нет :)
>>190694
Если объясняешь, то объясняй полностью. По-твоему, человек знает, что такое касательное пространство, но не знает, что такое дифференциал?
Общеизвестными можно считать только понятия множества, отображения, группы, линейного пространства, вещественных чисел и матрицы.
>>190397
это не вопрос терминалогии. это просто неправильно.
1-формы - это линейные функционалы на касательных векторах. т.е. они берут вектор и переводят его в число. дифференциал же берёт вектор и переводит его в другой вектор.
совпадение получается, например, когда функция переводит точку в число. ибо касательное пространство над числами - это такие же числа.
1-форма не является дифференциалом, скажем, вектор-функции (которая принимает значения в точках на R^n). А 2-форма не является дифференциалом уже никакой функции вообще.
более коротко: некоторые дифференциальные формы являются дифференциалами некоторых функций (а именно 1-формы - это дифференциалы функций со значениями в R).
>>190666
>имеется в виду, что не обязательно брать все возможные знаменатели
>имеется в виду
Ну и нахуй так жить? Вот в следующем же предложении опять НЕХ.
>Получающиеся при этом точки деления соответствуют «десятичным дробям». Так, числу 0,12 = 1/10 + 2/100 соответствует точка, расположенная в первом единичном интервале, во втором «подынтервале» длины 10−1, и именно она есть начальная точка третьего «подподынтервала» длины 10−2.
Что еще за начальная точка? Тут что имеется в виду, лол? При том, что там не одна даже сотая, а 2. Я стал уже думать, что это трудности перевода, но в оригинале тоже самое. Нет, просто кто-то сказал, что годная книга, но нахуй такую годноту и классику, если в каждом предложении нужно угадать, что хотел сказать писатель. Хуй знает, как вы ее читали.
>>190723
Ну, ОК, ладно. По дороге в школу понял про третий под-под-интервал, типа эта точка лежит на границе второй и третей сотых частей. Но один хуй даже от одного этого абзаца впечатление как будто авторы страдают дислексией. Нехотеть.
>>190729
По-моему, всё описано довольно прозрачно, а ты слишком придираешься. Авторы взяли на себя тяжелую работу: объяснить основы математики "на пальцах", так что не стоит строго судить.
>>190694
так я не объясняю, а отвечаю на вопрос "что это такое", а отвечаю потому, что все другие ответы - неправильные.
значит, я делаю хорошее дело, даже несмотря на то, что не объясняю ) разобрать, что такое касательное пространства, и как между ними действует дифференциал, не бог весть, как трудно. однако полезно знать, что разбирать надо именно это.
>>190745
>все другие ответы - неправильные.
Ничего подобного. Есть разные уровни объяснения и обобщения. То, что тебе пиздануло понтануться именно диффгемовским пониманием дифференциала (а точнее тогда уж, "дифференциала отображения"), нихуя не отменяет и не обесценивает классического определения дифференциала функции (присутствующего в стандартных вузовских учебниках по анализу функции одной или нескольких переменных, а не дифф. геометрии) как главной линейной части её приращения.
Человек задал конкретный вопрос - получил на него конкретный ответ >>190354. Прочие понторезы идут нахуй.
>>190745
Это как если на вопрос школьника "что такое вектор" вместо направленного отрезка предлагать ему класс эквивалентности кривых или дифференциальный оператор на скалярных полях.
>>190748
это называется струёй (jet) и не всегда естественно определенно
>>190749
касательный вектор только так и надо определять - как вектор скорости кривой (как оператор необязательно). объяснять классы эквивалентности необязательно, но вводить кривую это самое удобное.
конечно, тут есть двойственность между "слишком сложно" и "правильно". и я считаю, что "правильно" важнее. на самом деле сверхтрудного там и нету (если речь идёт о базовых понятиях).
например, говорить "вектор - это направленный отрезок" - это неправильно! из-за того, что меня очень много так учили, будто вектор - это направленный отрезок, я долго не мог понять потом настоящие определения. только в аспирантуре разобрался.
между тем, они совсем нетрудные.
>>190756
> тут есть двойственность между "слишком сложно" и "правильно". я считаю, что "правильно" важнее.
Этот тезис сходит из молчаливой предпосылки, что то, что формулируется на более простом языке - неправильно, ошибочно. Между тем это не так. Как уже было сказано, есть разные уровни объяснения, и разные значения терминов. Иначе на любой вопрос из какой-то конкретной области математики можно сразу же было бы сказать "а читни-ка теорию категорий / гомотопическую теорию типов / или чо там еще модно из области предельно общего хардкора". Это ответ? Нет. Это просто выебон, который выдается не с целью конкретно ответить на вопрос оптимально и доступно текущему уровню спрашивающего, а чисто ради самого выебона. Это в корне ущербный с методической точки зрения подход.
Ясно, что чувак, способный адекватно воспринять слова "отображение касательных пространств", с большой вероятностью не стал бы задаваться вопросом "что такое дифференциал" в столь наивной общей постановке (если не тролль, конечно). Возможно, он школьник или первокур, которому просто надо сдать зачет. Или техник/инженер/прикладник и.т.п (а возможно, вообще гуманитарий), которым хитровыебанная абстрактная математика выше уровня втузовских дифуров и матана просто нужна. И вот такому человеку, вместо того, чтобы нормальным доступным (и вполне понятийно замкнутым) языком объяснить на обычном матанском левеле интересующее его понятие, ему предлагается с головой погрузиться в хардкор и освоить внешние формы, (ко)касательные расслоения и джеты. Это мало того что прагматически нецелесообразоно его уровню и целям, так еще и попросту бесполезно, т.к. в обозримые сроки у него понимания не прибавится (зато отвращение появится) -- тупо из-за отсутствия базового порога вхождения в тему. Это типичный случай неоптимальной отсылки к избыточной информации в ситуации, когда более простого и базового понятийного аппарата вполне достаточно, чтобы корректно ответить на вопрос.
И да, повторюсь: классическое определение дифференциала как линейной части приращения функции (и связанные с этим понятия "2-й дифференциал", "инвариантность формы 2-го дифференциала" и т.п., имеющие совершенно определенный смысл в контексте курса стандартного математического анализа) -- не является неверным. Это никак не противорчеит тому, что оно имеет соответствующее обобщение/перетрактовку в рамках дифференциальной геометрии.
>>190763
>"инвариантность формы 2-го дифференциала"
1-го, конечно же!!! (Быстросамофикс, блять.)
(для тех, кто понимает, о чем идет речь. Интересно, много ли среди таковых тех, кто мыслит дифференциал только через джеты и касательные пространства)
>>190756
>касательный вектор только так и надо определять - как вектор скорости кривой
Касательный -- возможно, но тут речь шла о понятии вектора вообще (вне или до того контекста, в котором появляется слово касательный).
>например, говорить "вектор - это направленный отрезок" - это неправильно!
Вообще-то в качестве начальной интуиции ассоциировать вектор с направленным отрезком как раз методически вполне оправданно, потому что:
1) Изначально векторные величины как раз и возникли как то, что несет в себе интуицию направления .
2) В физике сплошь и рядом векторы имеют смысл геометрически ориентированных объектов (скорости, силы, напряженности полей).
3) Такое понимание вектора (дополненное понятие скалярного и векторного произведений) позволяет изящно решать ряд задач стереометрии и планиметрии, способствуя развитию навыков математического мышления.
4) Оно полезно для понимания того, откуда растут ноги у всех обобщенных определений вектора, имеющих место в линейной алгебре и дифференциальной геометрии -- все они так или иначе формализуют на том или иному уровне строгости и адаптации к контексту (многообразиям и пр.) изначальную интуицию вектора как геометрического объекта, задающего некую "величину" и "направление" (оно может быть в сколь угодно закавыченном смысле, но понятийное ядро именно таково).
>из-за того, что меня очень много так учили, будто вектор - это направленный отрезок, я долго не мог понять потом настоящие определения.
Не очень понимаю, чего тут сложного.
Сначала вектор как направленный отрезок. Операции (сложение, умножение, скалярное и векторное произведение). Физическо-механический и геометрический смысл (сложение векторов сил, например, или скоростей). Изящные доказательства геометрических теорем (например, теоремы косинусов) на векторном языке.
Далее -- аналитическая геометрия на плоскости и в пространстве. Вектор как столбец 2-х (3-х) компонент. Операции, все дела. Поверхности, касательные и нормальные векторы к ним.
Слкдующий шаг формализации -- вектор как элемент абстрактного линейного пространства. Интуиция направления наработана, теперь абстрагируемся от конкретики 3-мерного евклидова пространсва. Асиоматика скалярных произведений, норма, Коши-Буняковский, произвольная размерность. Линейные операторы, матрицы, квадратичные и билинейные формы, собственные вкторы и т.п. В качстве экзотики можно аффинную структуру ввести.
Далее -- тензорная алгебра: дуальные базисы, сопряженные пространства, тнензорное произведение, метрический тензор и т.п.
Далее -- многообразия. Касательный вектор - либо как вектор "скорости" на кривой, либо как геометричекий объект с заданным законом преобразования компонент (как часть общего определения тензора в стиле Ландафшица иил Рашевского), либо как линейный дифф. оператор на скалярных ф-циях на многообразии, либо как класс эквивалентных путей, и т.п. Опять же, интуиция направленного отрезка со всей естественной алгеброй операций и т.п. везде красной нитью проглядывается, и главное, понятно, зачем, где и почему удобно именно так.
По-моему, вся линия обобщения понятия вектора -- от направленого отрезка до прочего -- вполне логичная и стройная. Наоборот, гораздо более странным было бы, скажем, начинать сразу детишек учить векторам как элементам абстрактного линейного пространства или тупо как столбцам чисел, не потрудившись выработать у них наглядную пространственную интерпретацию.
Что вы тут за хуйню развели? Дифференциал -- это базисный ковектор кокасательного простарнства. Ясно, что он является один-формой, как и вектор является тензором первого ранга.
>>190768
а не базисный? а в каком базисе? а в другом базисе как? сам разберись, что пишешь
>>190766
речь шла о дифференциале, а дифференциал это отображение на касательных векторах. вектор вообще - это упорядоченный набор чисел (координат)
для меня был очень трудным переход от "направленный отрезок" к "класс эквивалентонсти кривых". я лично был бы рад переучиться, начиная с опеределния "вектор как элемент абстрактного линейного пространства"
>>190768
Выше уже ответили на это. Во-первых, если на то пошло, то не обязательно базисный (как насчет дифференциала функции?). Во-вторых, дифференциал - это не 1-форма (разве что только в жаргонном смысле обозначения "dx"). Если это дифференциал отображения - он переводит касат. пр-ва друг в друга (векторы в векторы). Если это дифференциал в классич. смысле анализа ф-ций 1-й переменной - тогда тем более аппарат форм тут как собаке пятая нога, т.к. ни на какие векторы при это действие вообще может не вводиться - и ничего.
>>190769
>вектор вообще - это упорядоченный набор чисел (координат)
Опять же тут есть нюансы. Физик, например, скажет, что не любой набор чисел образует вектор, а только такой, который преобразутся по тензорному закону при смене системы координат (напр., набор трех скаляров в этом смысле вектором не будет). А потом еще различие между полярными и аксиальными векторами введет.
>>190769
> а в каком базисе
Базисный вектор в базисе...
Да пошёл ты.
> на касательных векторах
а в каком базисе? а в другом базисе как? сам разберись, что пишешь
>>190771
Ну ясно, что определений можно дать массу. Если хоть чуть абстрагироваться от функции одной переменной, но не так сильно, чтобы асбтрагироваться от координат вообще, то определение, которое я привёл, вполне норм.
А так можно в рамках теории категорий определение дать, абстрагированное даже от пространств.
>>190768
И наконец, если тебе так нужно ассоциировать дифференциал с 1-формой - к твоим услугам понятие внешнего дифференциала, так что ты отвечаешь не на тот ответ.
>>190772
>полярными и аксиальными
Аксиальные векторы не нужны, это суть есть антисимметричные тензоры.
>>190775
Ну, ещё раз говорю, определений можно массу привести. В конце концов, производную и дифференциал можно определить тысячей способов. Есть даже арифметическая производная. Ещё можно приплести понятие из вариационного исчисления.
>>190776
> Аксиальные векторы не нужны, это суть есть антисимметричные тензоры.
Через дуализацию - это конечно да, но само разделение на "истинные" и "псевдо-" скаляры, векторы и тензоры (равно как и понятия тензорных плотностей некоторого веса) достаточно общее и вовсе не привязано к антисимметричным тензорам.
Нахер вообще это всё, когда есть теория категорий, в которой каждой громоздкой и неясной хуйне есть красивая и лаконичная аналогия?
>>190779
>Иначе на любой вопрос из какой-то конкретной области математики можно сразу же было бы сказать "а читни-ка теорию категорий
Хе, этот как раз иллюстрация к:
>Иначе на любой вопрос из какой-то конкретной области математики можно сразу же было бы сказать "а читни-ка теорию категорий
(Бля. Нутыпонял, короч.)
>>190780
А почему бы и нет? И главная плюшка в том, что теоркат -- это, вообще говоря, алгебра (абстрактная) стрелок. А алгебра проста для понимания, потому что в основе базируется на простых операциях.
Советую новичкам читнуть теоркат от Awodey
>>190783
>А почему бы и нет
Потому что теоркат -- это
> вообще говоря, алгебра (абстрактная) стрелок
Это форма, каркас. Наполнение конкретикой здесь отсутствует. На одной теории категорий коллайдер не расчитаешь, черную дыру не опишешь и квантовый компьютер не построишь.
>>190785
>А алгебра проста для понимания, потому что в основе базируется на простых операциях.
Теоретически - да. Практически - можно наслоить таких морфизмов и коммутативных диаграмм, что хуй втыкнешь, чо куда и почему. Сложность тоже ведь рзного типа бывает: понятийная легкость базовых понятий вполне может сочетаться с непроходимым лесом громоздкой их комбинаторики.
>>190785
Воу-воу, палехчи, товарищ.
Что такое "наполнение"? А чем "наполнены" конструкции "обычной" математики? Математика -- это наука о структуре и отношениях. Объекты без отношений иррелевантны.
Ясно, что для описания коллайдера нужны лишь алгебраические формулы, ДУ там, тервер и т.д.
Но для чего тогда вы тут ведёте такой длинный разговор об абстракциях дифференциала?
>>190787
>Ясно, что для описания коллайдера нужны лишь алгебраические формулы, ДУ там, тервер и т.д.
Вот это и есть то наполнение, которое в самой теории категорий отсутствует (ибо как было сказано, ее суть в том и состоит, чтобы предельно абстрагироваться от всего этого,поднявшись до уровня чистых выхолощенных формальных стрелок и функторов). А хочешь конкретики - будь добр опустись с этих вершин до уровня конкретной категории - линейных пространств, топологических пространств,групп и т.д., со своим конкретным и специфическим языком.
>>190787
>Но для чего тогда вы тут ведёте такой длинный разговор об абстракциях дифференциала?
Потому что здесь налицо столкновение двух подходов к объяснениям в математике: "хардкор и только хардкор" и "релевантность порогу вхождения".
>>190783
>это, вообще говоря, алгебра (абстрактная) стрелок. А алгебра проста для понимания, потому что в основе базируется на простых операциях
Вот действительно, смотрю -- куда уж проще-то?
>>190790
Немного уточню понятия.
Класс задач - это такие задачи, возникающие в разных предметных областях, которые с помощью абстракции можно свести к одной и той же формальной задаче.
Проблема - это задача, которую человек не может решить.
Класс проблем - это класс задач, в который входит данная проблема.
Конкретное объяснение - это множество действий, которые нужно совершить над данным человеком, чтобы сделать его способным решить данную проблему.
Общее объяснение - это множество действий, которые нужно совершить над данным человеком, чтобы сделать его способным решить любую проблему из класса проблем, в который входит данная проблема.
Каждое действие совершается за некоторое конкретное количество времени, причём обладается свойство аддитивности.
Время объяснения - количество времени, которое требуется для совершения действий, входящих в объяснение.
Предпочтительное объяснение - это объяснение с наименьшим временем объяснения.
Здесь спор о том, что нужно по умолчанию делать с человеком, столкнувшимся с проблемой: давать ли ему предпочтительное общее объяснение или же давать ему предпочтительное конкретное объяснение.
Я предлагаю поступать так. Если время предпочтительного общего объяснения не более чем в полтора раза больше времени предпочтительного конкретного объяснения, то давать нужно предпочтительное общее объяснение. В противном случае нужно давать предпочтительное конкретное объяснение.
Возникает вопрос: как определить время объяснения? Предлагаю считать, что понимание каждого понятия происходит за одно и то же количество времени. В таком случае время объяснения эквивалентно количеству понятий, которые вводятся в объяснении.
>>190819
Прикольно.
Но нужно учитывать тот эффект, что носители общих (и только лишь общих) определений зачастую хуже решают конкретные проблемы, чем носители конкретных определений. Пример: любители общих определений тензоров через алгебраико-категорный язык бывают не в состоянии вычислить конкретный метрический тензор на сфере, например (а иногда даже осознать, что от них вообще требуют).
Поэтому чтобы твой термин "общее объяснение" действительно включал в себя способность обучающегося обрести при этом навык решения не только общих, но и конкретных задач за оптимальное время, данное объяснение должно сопровождаться и усвоением алгоритмов перехода к уровню более узих конкретных определений и операций с ними, прагматически целесобразных для уровня данных конкретных задач.
Да и если у чувака на зачете вопрос "сформулируйте понятие 2-го дифференциала функции одной переменной, вычислите его для конкретной функции и объясните, что означает слова неинвариантность формы 2-го дифференциала", я бы посмотрел, как ты предложишь чуваку готовиться к ответу на этот вопрос через освоение струй и касательных расслоений.
>>190832
Нахуя вообще зачеты (спросим по большому счету)? Риторический вопрос.
>>190791
> куда уж проще-то
Просто, когда знаешь правила "рисования" стрелок. Я вообще задумался, что можно программу по типу поиску по графу написать, которая сама будет считать композиции, UMP, экспоненциалы, пуллбэки и прочая и искать изоморфизмы там и так далее. Потому что задача кажется алгоритмизуемой.
>>190826
И, да, вы ещё упускаете такой момент, что только с помощью языка теорката и теории типов (насколько нам ПОКА известно) можно создать программы, которые в состоянии доказывать "конкретные низкоуровненвые", "материальные", если хотите, теоремы матанализа. Построение метрических тензоров, думаю, задача нетривиальная, т.к., вообще говоря, нужна параметризация (произвольного) пространства. А это, скорее всего, NP-полная задача.
>>190836
Тред плавно съезжает с катушек к Воеводскому (который тоже слегка без катушек)
>>190838
Ладно. Итог таков. На любой вопрос любого студента тех.вуза по матану 1-го семестра будем отвечать "сосни теорката, тупорылое уебище".
>>190802
При чём тут иррациональные? Мы покрываем всюду плотным множеством рациональных чисел, используя только степени 10 в качестве знаменателя.
Разложить на множители x^5+1
>>191035
Кури теорию колец и roots of unity. По рабоче-крестьянски никто это не делает.
>>191051
Авторы советуют что-нибудь отнять и вычесть, а есть чо почитать по кольцам?
>>191037
Вообще как я понял это из предположения, что выражение обращается в ноль при х=-1, поэтому х+1 один из множителей, а второй создан так, чтобы уничтожать остальные побочные члены. Второе какой-то лимб, не знаю как до этого додумываться.
>>191063
(Вообще это просто пиздец. Скоро наверное в дважды девять без калькулятора не смогут. А интеграл от синуса будут месяц брать.)
>>191064
Я даже боюсь об интегрировании по частям спрашивать.
>>191064
Деление многочленов в столбик? Ох, и не помню когда я этим занимался. Продемонстрируй класс:
(x^5+1)/(x-1)
>>191100
ну это очень легко, так же как и с обычными числами.
сейчас я расскажу, как это делается!
x^5+1 надо представить как x^5+0+0+0+0+1, где нулями обозначены пропущенные степени x
далее, сначала умножаем (x-1) на x^4 (чтобы сократилась пятая степень)
вычитаем x^5+0+0+0+0+1 - x^4(x-1)
из того, что осталось вычитаем x^3(x-1) с коэфициентом (чтобы убилась четвертая степень)
и т.д.
>>191100
Я тоже хуй знает сколько этим не занимался.
>>190406
Я спрашивал про другую сумму. Пикрилейтед. Если обе суммы эквивалентны и имеют по n слагаемых, где теряется последнее слагаемое второй суммы?
>>191302
То есть, по сути формула должна быть такой:
2*S = 1-1+1-1+1-...+n
или
2*S = 1-1+1-1+1-...-(n+1)
>>191199
>zx^2+yx^2+yz^2+xz^2+zy^2+xy^2
разложить на множители? красиво не получится, по-моему
>>191384
Должно быть красиво, вот я думаю. Предположу, что можно доделать формулу суммы квадрата с помощью +что-то -что-то.
Анон, подскажи годную книжку по статистике, желательно для идиотов.
Или по языку R, но уже совсем для имбецилов.
>>191412
ВольфрамАльфа не разложил, так что вряд ли там что-то хорошее можно сделать.
>>191434
Вольфрам альфа не умеет брать простейшие кратные интегралы, так что это ничего не значит.
>>191434
Лол, ну это же олимпиада для школьников, почему школьники могут, а я нет.
>>191462
Что за олимпиада для школьников с таким заданием? Поделись-ка.
Есть некоторое количество произвольных чисел
ABCD
Какое ассоциативное действие нужно совершить над A и B, чтобы получить C, не зависимо от их значения?
Какое ассоциативное действие нужно совершить над B и C, чтобы получить D, не зависимо от их значения?
Какое ассоциативное действие нежно совершить, чтобы восстановить последовательность?
Например
C = A + B
B = C - A
D = A?B?C
С = D?A?B
A = D?B?C
B = C?A?D
>>191551
>Какое ассоциативное действие нужно совершить над A и B, чтобы получить C, не зависимо от их значения?
C = F(A,B) = 0
>Какое ассоциативное действие нужно совершить над B и C, чтобы получить D, не зависимо от их значения?
C = F(B,D) = 0
Ставь задачи нормально, аутист.
Имеется n сплетниц, каждая из которых узнала новую сплетню и спешит ею поделиться. Они звонят друг другу и обмениваются всеми новыми сплетнями. Сколько нужно звонков, чтобы все узнали все сплетни?
>>191868
Если они услышав очередную сплетню тут же обзванивают друг друга, то формула усложняется, пространственно временной континуум сжимается и делится всё на 0.
Короче.
Две сплетницы в любой момент времени заняты, тоесть (n/2) и получаем узнающих очередную сплетню, вторая половина сплетню рассказывает.
Они узнают единственную сплетню, но, так как они обязаны за один звонок рассказать новые сплетни друг другу, то они меняются ролями, а мы снова делим на 2 наших сплетниц, так, как сплетен становится в двое больше за звонок. (n/4)
n/2 количество обменивающихся сплетниц
n/4 количество сплетен
При этом количество сплетен уменьшается в два раза при каждом одновременном звонке сплетниц, как и количество сплетниц, которым эта сплетня нужна, а это значит, что берём цикл z от 0 до +шта c шагом 1, в котором Е количество звонков:
Е(n) = (n/(z*2))*(n/(z^2))
Тут я уверен, что ошибся, во первых по тому, что формулы писать не умею, во вторых проверить или доработать мне желания не хватит.
>>191872
Я думаю речь идет о необходимом и достаточном количестве.
Не уверен, что в подходящий тред зашёл, и вообще в тот ли раздел, но у меня вопрос по формулировке темы к.ф.-м.н. диссертации. Дело в том, что и материал диссертации практически готов, и статейки ВАКовские в нужном количестве уже имеются (канд. экзамены тоже сданы). Но проблема в том, дадут ли защищать алгоритм и его расширения -- ну конечно дадут, но можно ли название диссертации иметь как <Прилагательное> алгоритм blah-blah...?
От кого-то слышал, что нельзя алгоритмы защищать, а уж тем более для кандидата физико-математических наук.
>>191941
Воу-воу. Это почему это нельзя?
http://www.math.spbu.ru/user/mbk/D21223251/Thesises.html
Гляди, сколько там алгоритмов.
>>191948
Алсо, thesises. Обосрался, блядь, и смех, и грех.
Это всё к тому, что рашконаука будто и не вылезала из-за железного занавеса.
>>191786
Очевидна стратегия типа разделяй и властвуй. Нужно поделить сплетниц пополам, каждая половина обменивается сплетнями, затем группы объединяются посредством N/2 звонков. F - количество звонков. F(1) = 0, F(2 * N) = F(N) + F(N) + N.
F(2) = 0 + 0 + 1 = 1
F(4) = 1 + 1 + 2 = 4
F(8) = 4 + 4 + 4 = 12
F(16) = 12 + 12 + 8 = 32
F(32) = 32 + 32 + 16 = 80
F(64) = 80 + 80 + 32 = 192
F(2N) = 2F(N)+X
F(N) = (F(2N)-X)/2
Кто хочет, может решать дифуру, но решение "угадывается" легко.
F(N) = N * (log2(N)/2)
Для N некратных степеням двойки в расчеты надо вставлять всякие ]N/2[ и подобное говно, а потом муторно все считать. Мне в лом. Думаю получится один хер N * ] (log2(N)/2)[ какое-нибудь.
>F(2N) = 2F(N)+X
>F(N) = (F(2N)-X)/2
Очевидно вместо X я хотел написать N
>N некратных степеням двойки
А тут я хотел написать "N неравных степеням двойки". Ну вы понели.
>>191953
>F(32) = 32 + 32 + 16 = 80
не может быть.
Отделяем одну альфа-сплетницу, остальные докладывают ей все сплетни. Это займет 31 звонок.
Затем альфа-сплетница звонит всем в обратном порядке, это еще 30 звонков.
61 звонок перебором, а у вас 80.
>>191969
Ага, я соснул. Все верно. Я соснул. Сейчас подумаю как объединять две группы меньше чем N/2 звонками.
Потсоны, я тупейший мудак, мне нужно сдать ещё 5 предметов (я их знаю), но в математике я нуб, и если не сдам — останусь на второй таки год, а я не хочу, помогите, позязя.
Если не трудно, объясните по каким принципам и правилам решали это не обязательно, ибо я и так охуел.
>>191969
Что-то мне начинает казаться что начиная с N=9 альфа-сплетница - лучшая стратегия. Но доказать я этого не могу.
>>191869
Как это? Каждая звонит как минимум раз, чтобы рассказать свою новость (n), и как минимум один раз принимает звонок со всеми новостями (n). Откуда -3?
>>191981
Да я не знаю какие и задать.
Мне нужны решения хотя бы четырёх заданий (там видно, это на трояк), хотелось бы, конечно, решения всех.
Но боюсь закидаете говном за охуевание.
>>191987
1. Альфа-сплетница звонит всем это (n-1) звонков
2. Альфа-сплетница звонит всем в обратном порядке, и еще минус последняя сплетница из первой группы звонков, т.к она уже все слухи знает. (n-2)
2n-3
Но это только верхняя граница, можно меньше.
>>191988
Правильно боишься. Но плюс уже за то, что не пробуешь получить решения, не пошевелив мозгами. Поэтому я отправляю тебя в увлекательное путешествие Википедией: http://ru.wikipedia.org/wiki/%D0%A2%D1%80%D0%B8%D0%B3%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%87%D0%B5%D1%81%D0%BA%D0%B8%D0%B5_%D1%84%D1%83%D0%BD%D0%BA%D1%86%D0%B8%D0%B8 , особое внимание обрати на так называемое основное тригонометрическое тождество, оно тебе поможет несколько раз.
>>191989
Действительно. Я считал столбы, а не промежутки.
Но меньше вряд ли можно, так как нужно, чтобы больше двух сплетниц получили лишь один звонок и узнали все новости.
>>191990
Боже, я испытываю страх и ужас от этих формул, это тождество и в тетрадочке есть, думал, есть что попроще, так сказать для гуманитариев.
Куда направишь для решения задачи №4?
>>191991
Вот для случая n=4 можно за n звонков, например
>>191992
Для четвертой задачи хорошо бы представить все это, а лучше нарисовать. Ну и это не помешает http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D1%8F%D0%BC%D0%BE%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D1%8B%D0%B9_%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA
И не верю я в гумунитариев. Понять школьную математику под силу каждому. Ты сталкиваешься с подобными вещами каждый день, просто тебя не научили проводить правильные аналогии.
>>191993
У твоего варианта сложность n*log(n), если я все правильно рассмотрел, что хуже линейного варианта для больших n, которые обычно фигурируют в таких задачах.
>>191995
Это просто пример, нас-то просят найти лучшее решение для любых n.
>>191997
Это разве что в виде «для таких-то n такая-то стратегия».
>>191875
Решил, проверил m=n*2, где m - количество звонков для n > 4 и при условии, что каждая сплетница звонила каждой и обязательно узнавала и рассказывала все сплетни которых не знала одна из связавшихся сплетниц.
n|m
2|1
3|3
4|6
5|10
6|12
7|14
а дальше я не проверял
>>191994
>а лучше нарисовать
Да я нарисовал, вообще думал, что это самое простое задание. Ну и люто на нём обосрался.
А как мне поможет треугольник? Там жи плоскость.
>И не верю я в гумунитариев
Верь.
>Понять школьную математику под силу каждому
Возможно, но я кроме простейших уравнений и многочленов нихрена не понимаю. А от геометрии вообще прячусь в угол и плачу как девчонка.
Сейчас вот сидел, пытался решить первые четыре задания, смог только в 3, и то благодаря гуглу.
>>192006
Смог же.
По поводу четвертой. Нужно начать из того, что паралельные прямые лежат в одной плоскости (их свойство), CD тоже в ней (очевидно, стоит ли это доказывать?). Теперь твой рисунок будет похож на N. С ним работать попроще.
>>192000
Ну давайте хотя бы составим таблицу минимального количества звонков от n.
n - кол-во звонков
1 - 0
2 - 1
3 - 3
4 - 4
5 - 7
6 - 8
7 - 11
пока верно?
Хелп, искал лок.экстремумы в функции нескольких переменных - посчитал гессиан (Матрицу Гессе), а он нулю равен.
Что дальше прикажете делать, аноны? Сечение плоскости строить и оттуда точку выковыривать?
>>192035
Математики... Такие математики.
Пойду отсюда, пожалуй.
>>192060
Что на чертеже непонятно-то, лол? горизонтальная линия -- плоскость (если смотреть "сбоку, в торец"), остальные -- исходные прямые, её пересекающие.
>>191948
Спасибо, аж полегчало. Я стану полковником к.ф.-м.н.
А все самые сложные проблемы теории чисел сводятся к сложению простых чисел, ну или хотя бы просто связаны с простыми?
А я все еще не могу решить олимпиадную задачку. Неужели я такой дебил:
xy^2-xz^2+yz^2-yx^2+zx^2-zy^2=
разложить на множители
>>193046
> Неужели я такой дебил
да (в прошлый раз вместо минусов плюсы были)
я тоже дебил (сам не сумел, вольфрама спрашивал)
Что значит n! ?
>>187741
задачка на топологию/логику:
есть три студента нищеброда, они сняли одну шлюху, но при этом у них всего два презерватива на троих, при этом каждый студент болен какой-то венерической болезнью, а шлюха больна каким-то своими.
опишите алгоритм действия с презервативами, чтобы каждый студент потрахался, но при этом никто ничего бы друг от друга не подцепил.
>>193334
ЛОЛ. Каждый раз с него проигрываю. Всегда представляю, что было бы если бы препод поехал и стал лекции таким образом читать.
>>193314
1-й студент надевает 1-й презерватив и на него 2-й
2-й студент выворачивает 1-й презерватив и надевает на него 2-й.
3-й студент вытаскивает 1-й презерватив из 2-го и использует только 2-й.
>>193462
В результате третий подцепил трипак от первого.
>>193474
1-й студент надевает 1-й презерватив и на него 2-й
2-й студент вытаскивает 1-й презерватив из 2-го и использует только 2-й.
3-й студент выворачивает 1-й презерватив и надевает на него 2-й.
>>193372
Это сейчас модно всех называть поехавшими, кого понять не в состоянии?
Соединить дома, которые находятся в вершинах квадрата со стороной в 1000 м дорогами так, чтобы общая протяженность дорог была наименьшей.
>>193497
Ну в общем, как-то так.
>>193498
А, не, туплю, конечно же вот так.
Есть тридиагональная матрица с известными разными коэффициентами, параметризованными каким-то числом (что исключает численное решение). Как вообще решать задачу на собственные значения такой матрицы?
>>193502
Ноуп. Должно быть как-то так. Но углы вычитывать, кому не впадлу может искать минимум такой конфигурации.
>>193509
>очевидно
А ты линейкой померяй, долбоёб. Очевидно ему, блять.
>>193557
Более того, при соединении любого количества произвольно разбросанных точек на плоскости вот таким минимально коротким образом, все дополнительные узлы, если они будут, всегда будут представлять из себя схождение трёх лучей под углом 120°
>>193557
А теперь та же задача для шести точек двумя рядами вот так:
* * *
* * *
Ну то есть два квадрата с общей стороной.
>>193580
Пробелы проебались. Два квадрата с общей стороной, короче.
* * *
* * *
Рисунок сделаю если до ответа никто не додумается.
>>193505
>Как вообще решать задачу на собственные значения такой матрицы?
Так же как и задачу на собственные значения любой другой квадратной матрицы: найти из уравнения Ax=λx.
>>193579
А вот это довольно сильное утверждение, попробую доказать или опровергнуть.
>>193607
А я уже опровергнул. Не может тут быть лучей. Только отрезки.
>>193557
Хуй знает, я считал через Вольфрам, получил 110° (между «вертикальными» линиями). Это он настолько наебывает?
Помогите глупцу. Я умею решать задачи по теории вероятностей(Классическая теория, сложение и умножение, Бернули и т.д.). Но вот определить тип для меня сложновато, подскажите, как на лету определить тип конкретной задачи?
>>187962
>1 банан = 7 обычным бананам
Уточни. Если по весу - то первую, ибо вес пачки фиксированный. Если по пищевой ценности то пофиг.
>>193587
Если под MST ты подразумеваешь минимальное остовное дерево то у меня для тебя плохие новости: перересток можно устроить где хочешь, так что здесь это не прокатит.
>>193641
По пищевой ценности. А вообще данных недостаточно для решения. Такой вот ответ.
Сколько клеток пересекает диагональ в клетчатом прямоугольнике размерами NxM (N, M натуральные)?
Пытаюсь доказать, что N+M-(N,M). Понятно (по диофантову уравнению диагонали), что диагональ пересечёт (N,M)-1 узел. Но почему если диагональ не пересечёт ни одного узла (т.е. (N,M) = 1), то она пересечёт N-M-1 клетку?
И вообще: какими рассуждениями семиклассник решает такую задачу: "Сколько клеток пересекает диагональ в клетчатом прямоугольнике размерами 199 × 991?"?
>>193710
>все пересечения мы можем посчитать как число пересечений с диагональными + число пересечений с вертикальными
Не понял. Что ты имеешь в виду под "диагональными" и "вертикальными"?
Есть последовательность натуральных чисел:
a1, a2, a3, a4 ... an
Над последовательностью проводится процесс по следующему принципу:
произвольно выбирается пара чисел из последовательности таких, что левое не делит правое, скажем a3 не делит a7.
Левое число заменяется на наибольший общий делитель пары чисел, скажем, gcd(a3, a7), а правое -- на наименьшее общее частное, скажем, lcm(a3, a7).
Далее эти действия повторяются.
Показать, что такой процесс для данной последовательности остановится и его результат (результирующая последовательность) не зависят от начального шага.
А есть какое-нибудь общепринятое название функции произведения первых n простых?
f(5) = 2 * 3 * 5 * 7 * 11 для примера
По определению можно положить f(0) = 1, очевидно.
Есть примориал -- это произведение всех простых простых чисел <= n:
12# = 2 * 3 * 5 * 7 * 11
, но это не то. Мне нужно чтоб именно количество первых простых являлось аргументом.
Наверняка много учёных в мире испытывали потребность в такой функции, а я не могу нагуглить ни по-русски, ни по-английски в википедии не написано. Можно ссылочку на какое-то устоявшееся название в английской или русской литературе?
Сука, как же я заебался с этим говном!
Нужно, блядь, найти объем вращения тела вокруг оси Ох, черт её побери, заданного y=x^2 * e^(-x^2), и y=0. Тут, мать его, Пуассон вылазит наверное, но я хуй знает, ибо не проходили это говно.
Если кто решит, буду благодарен. Ну могу еще 5$ кинуть, если с решением напишите куда кидать и объясните как, ибо у меня только VISA есть, а больше ничего.
>>193812
Погугли, может, в сторону euler totient function
>>193812
Это и есть примориал, просто его определяют по-разному
http://mathworld.wolfram.com/Primorial.html
http://en.wikipedia.org/wiki/Primorial
>>193747
Заметим, что длина каждой цепочки преобразований не превосходит n^2. Для этого докажем, что число пар индексов по которым можно провести преобразование уменьшается после каждого преобразования. Действительно, после преобразования по индексам (k1,k2) для всякого l=/=k1,k2 число пар вида (l,ki) или (ki,l) по которым можно проводить преобразование не возросло. Последнее может быть доказано несложным перебором случаев взаиморасположения l, k1, k2.
Дальше один из путей - это указать явный вид конечного результата, показать, что он сохраняется под действием преобразований и что для любой последовательности, не совпадающей с конечным результатом, имеется допустимое преобразование. Я пойду другим путём и покажу, что все цепочки преобразований приводят к одному конечному результату без указания явного вида этого результата.
Покажем, что для всяких k, l, r, t от 1 до n и (b1,...,bn) существуют две цепочки преобразований из (b1,...,bn) с одинаковым результатом такие, что первая начинается с (k,l), а вторая с (r,t). Имеются два нетривиальных симметричных случая: 1. k<l=r<t и 2. r<t=k<l. Без ограничения общности разберём только первый. Рассмотрим цепочки (k,l),(l,t),(k,t) и (l,t),(k,l),(k,t). Выкинем из них пары индексов по которым нельзя провести преобразование в соответствующий момент. Несложно убедится, что в результате преобразований из (b1,...,bn) по обоим цепочкам на k-ом месте будет ck=gcd(bk,bl,bt), на t-ом будет ct=lcm(bk,bl,bt) и на l-ом будет cl=(bk*bl*bt)/(ck*ct).
Будем говорить, что (b1,..,bn) хорошая последовательность, если конечный результат преобразований из неё не зависит от выбора цепочки. Будем говорить, что допустимая из (a1,...,an) цепочка преобразований (k1,l1)(k2,l2)...(km,lm) хорошая, если результат преобразований по ней из (a1,...,an) хороший и будем говорить, что она плохая, иначе. Если все цепочки хорошие, то в частности пустая цепочка хорошая и мы доказали требуемое. Предположим, что плохие цепочки есть. Рассмотрим плохую цепочку (k1,l1)(k2,l2)...(km,lm) максимальной длины. У неё есть два хороших продолжения (k1,l1)...(km,lm)(r1,t1) и (k1,l1)...(km,lm)(r2,t2) для которых предопределены разные финальные результаты преобразований. Но заметим, что в силу доказанного в предыдущем абзаце у них есть продолжения с одинаковым результатом, а следовательно и финальные результаты для них совпадают - противоречие с предположением существования плохих цепочек.
>>193856
> Имеются два нетривиальных симметричных случая: 1. k<l=r<t и 2. r<t=k<l
А почему только эти, а не, например, k<l<r<t или k<r<l<t? Требуется пояснение, почему эти случаи тривиальные. Например, почему алгоритм приведёт к одинаковому результату, если мы начнём с двух крайних и двух "внутренних" членов.
> Рассмотрим цепочки (k,l),(l,t),(k,t) и (l,t),(k,l),(k,t).
Остальные тоже надо разобрать и включая вышеозначенные случаи.
> У неё есть два хороших продолжения (k1,l1)...(km,lm)(r1,t1) и (k1,l1)...(km,lm)(r2,t2) для которых предопределены разные финальные результаты преобразований.
Тогда это "плохие" цепочки согласно определению.
> Но заметим, что в силу доказанного в предыдущем абзаце у них есть продолжения с одинаковым результатом, а следовательно и финальные результаты для них совпадают - противоречие с предположением существования плохих цепочек.
Совершенно не ясно, как из абзаца 3 следует утверждение абзаца 4, требуется пояснение или другое доказательство.
>>193910
И сразу outline другого варианта (пока без деталей).
1. Легко видеть, что a1 участвует в преобразованиях до тех пор, пока не станет gcd(a2, a3, ... an)
2. После этого a1 больше не участвует в преобразовниях независимо от их дальнейшего хода, назовём его "стабилизированным"
3. Назовём это "шагом" алгоритма
4. Ясно, что алгоритм проделывает n-1 шагов
5. Можно показать, что переход от одного шага к следующему осуществляется заменой первого нестабилизированного элемента на gcd всех правых и только ею
Есть ли такие функции, что df(x)/dx = f(x), кроме exp(x), и если нет, как это доказать?
>>193916
Да, есть. Например, 2*e^x. Аккуратнее нужно условия формулировать.
>>193910
>А почему только эти, а не, например, k<l<r<t или k<r<l<t?
В остальных случаях, кроме совсем тривиального k=r, l=t, преобразования (k,l) и (r,t) коммутируют и соответственно подходят цепочки (k,l)(r,t) и (r,t)(k,l).
>Остальные тоже надо разобрать и включая вышеозначенные случаи.
Я доказывал существование пары цепочек требуемого вида, а в рассматриваемом случае эти подходили.
> >У неё есть два хороших продолжения (k1,l1)...(km,lm)(r1,t1) и (k1,l1)...(km,lm)(r2,t2) для которых предопределены разные финальные результаты преобразований.
>Тогда это "плохие" цепочки согласно определению.
Имелось ввиду что есть однозначный финальный результат для первой цепочки (b1,...,bn), однозначный финальный результат для второй цепочки (c1,...,cn), но при этом они не совпадают, т.е. для некоторого k имеем bk=/=ck. Сами эти цепочки не могли быть плохими т.к. они имеют длину большую, чем максимальная по длине плохая цепочка.
>Совершенно не ясно, как из абзаца 3 следует утверждение абзаца 4, требуется пояснение или другое доказательство.
Пусть результат применения (k1,l1)...(km,lm) (максимальная по длине плохая цепочка) к (a1,...,an) равен (b1,...,bn). Тогда найдём, согласно доказанному в абзаце 3, цепочки (r1,t1)(k'1,l'1)...(k'm',l'm') и (r2,t2)(k''1,l''1)...(k''m'',l''m'') такие, что при применение к (b1,...,bn) они обе дают некоторую последовательность (c1,...,cn). Рассмотрим некоторую цепочку преобразований (e1,w1)...(ep,wp), которая при применение к (c1,...,cn) даёт последовательность к которой уже нельзя применять преобразований. Обозначим этот результат через (d1,...,dn). Теперь имеем, что у (k1,l1)...(km,lm)(r1,t1) и (k1,l1)...(km,lm)(r2,t2) есть продолжения (k1,l1)...(km,lm)(r1,t1)(k'1,l'1)...(k'm',l'm')(e1,w1)...(ep,wp) и (k1,l1)...(km,lm)(r2,t2)(k''1,l''1)...(k''m'',l''m'')(e1,w1)...(ep,wp), соответственно. При это эти продолжения при применение к (a1,...,an) дают одинаковые финальные результаты - (d1,...,dn). Последнее противоречит тому, что (k1,l1)...(km,lm)(r1,t1) и (k1,l1)...(km,lm)(r2,t2) имели различные финальные результаты.
>>193911
>1. Легко видеть, что a1 участвует в преобразованиях до тех пор, пока не станет gcd(a2, a3, ... an)
Наверно, здесь должен был быть gcd(a1, a2, ... an).
>5. Можно показать, что переход от одного шага к следующему осуществляется заменой первого нестабилизированного элемента на gcd всех правых и только ею
Это должно сработать. Но после 5. для того, чтобы завершить доказательство ещё нужно доказать, что gcd всех правых не зависит от конкретного вида предшествующих шагов.
>>193922
Лол. Но ты меня понял и не ответил.
Похоже, что нет, так как если эту функцию разложить в ряд Тейлора, то мы должны получить ряд, соответствующий экспоненте.
>>193928
Воспользуйся теоремой о существования и единственности решения задачи Коши.
>>193927
> Наверно, здесь должен был быть gcd(a1, a2, ... an).
Да, опечатался.
> Это должно сработать. Но после 5. для того, чтобы завершить доказательство ещё нужно доказать, что gcd всех правых не зависит от конкретного вида предшествующих шагов.
Это легко видеть из того, что алгоритм не меняет общий gcd подпоследовательности:
например, для индексов i и j, не равных 1,
gcd(a2,a3 ... an) =
gcd(a2,a3 ... gcd(ai,aj) ... lcm(ai, aj) ... an)
С другой стороны, видим, при i=1 элемент aj остаётся прежним или домножается на натуральное число, что также не меняет gcd(a2,a3 ... an).
>>193926
> преобразования (k,l) и (r,t) коммутируют и соответственно подходят цепочки (k,l)(r,t) и (r,t)(k,l)
> Я доказывал существование пары цепочек требуемого вида, а в рассматриваемом случае эти подходили.
Хорошо, значит, если мы всегда будем брать тройки требуемого вида, то результат будет однозначен.
> Сами эти цепочки не могли быть плохими т.к. они имеют длину большую, чем максимальная по длине плохая цепочка.
Эти -- это цепочки уже из (b1,...,bn) и (c1,...,cn), я так понял?
Так, я ещё раз внимательно прочёл доказательство, но, сказать честно, я не вижу, как можно показать единственность результата таким образом. Через "плохие" и "хорошие" цепочки слишком tricky получается. Когда я читаю доказательство у меня ощущение Мюнгхаузена постоянно. Получается, плохая цепочка есть, но раз она максимальной длины, то дальнейший результат сам собой предопределён и не нужно вообще приплетать третий абзац. Я не отрицаю, что это рабочее доказательство, но, пожалуй, не для меня. Мне мне не ясен переход от существования "хороших" цепочек к существованию их и только их.
> при применение
Ах, таки спалился :)
Кстати, в варианте с gcd всех правых можно точно указать конечный результат и провести аналогию с invariant factor decomposition для конечных абелевых групп.
>>193961
> С другой стороны, видим, при i=1 элемент aj остаётся прежним или домножается на натуральное число, что также не меняет gcd(a2,a3 ... an).
Опечатался, сейчас исправлю.
>>193963
С другой стороны, видим, при i=1 элемент aj остаётся прежним или домножается на натуральное число и, соотвественно, gcd(a2,a3 ... an) остаётся прежним или домножается на натуральное число, то есть не убывает. Но gcd(a2,a3 ... an) <= lcm(a1, a2,a3 ... an) и, следовательно, сходится к единственному значению.
Halp. У меня тут немного перегрелись мозги.
1) В первый день вероятность события 20%.
2) Если события не произошло, то в следующий день вероятность увеличивается на 5% (до 25%), и так по +5% добавляется до максимума в 95%, после чего не растет.
3) Если событие произошло, то в следующий день вероятность падает обратно к 20%.
Как рассчитать (без тупого брутфорса, блеать) вероятность какого-то количества событий за разное количество дней (от 5 до 100)?
Брутфорс: тупо загнать алгоритм в прогу и оставить на ночь вычислять количество событий.
>>193968
x=0.2
в первый день вероятность х
во второй день вероятность хx+(1-х)(х*1.05) - с вероятностью х событие случилось и случится снова с вероятностью х, с вероятностью 1-x оно не случилось и теперь шанс его стал в 1.05 раз больше
в третий день (хx+(1-х)(х1.05))*x+(1-(х*x+(1-х)(х1.05))(хx+(1-х)(х*1.05))*1.05
Осталось эту последовательность запихнуть в алгоритм
что-то вроде X1, X2, X3, Xn, где Xn=Xn-1*х+(1-Хn-1)*x*1.05^n
вроде бы так
а вот на том, как этот ряд суммировать, я ломаюсь
>>193999
У тебя во второй день вероятность чего:
- того, что выпадет событие во второй день или в первый?
- того, что выпадет событие не в первый, а только во второй?
>>194002
ну смотри, у нас есть несовместимые события - вчера событие случилось и сегодня повторяется и вчера события не случилось и сегодня оно случилось
соответственно, вероятность, что случилось или одно или второе равна сумме обоих вероятностей
поэтому мы в энный день просто складываем вероятности обоих исходов - вероятность одного Xn-1*х, а вероятность второго (1-Хn-1)*x*1.05^n
АААА, бля, понял, где проебался
(1-Хn-1)*x*1.05^n - не может тут быть 1.05x^n
потому что неясно, как давно у нас не было событий и на сколько возросла их вероятность из-за этого
то есть не в степени n, а надо еще и эту степерь как-то рассчитывать, исходя из вероятностей
на этом моя математика сломалась
>>191786
Бампану задачу, т.к. до сих пор не решили. Может кто-то встречал её где-то ещё и укажет, как гуглить.
>>194019
Недостаточно информации же. Сколько сплетен за 1 звонок передается? Тратится ли одинаковое количество времени на передачу каждой сплетни? ... и т.д.
>>194004
Подозреваю, что придется пилить программу, которая вручную переберет все 2^n комбинаций возможных событий и из них отсортирует вероятности.
Олсо. Брутфорс не взлетел. Либо рандом корейский, либо сказалось мое незнание питона (изучаю его как раз).
По крайней мере, во время теста на 7 дней моя прога стабильно выдавала ~2.6% на "нет событий" вместо кошерных 4.5%.
0,8*0,75*0,7*0,65*0,6*0,55*0,5
>>194019
Тебе нужно уточнить как именно они звонят друг другу.
Не знал, куда задать этот ебанутый вопрос.
Допустим, мы выиграли 5 машин из 10 машин. 5\10 то есть. Значит, мы выиграли 50% машин.
Если мы выиграли 10 машин из 10 машин, то будет 10\10 и будет 100% выигранных машин.
А если мы выиграли 0 машин из 0 машин? 0\0 равно Аллах Бабах или все таки 100% выигранных машин?
>>193968
Дело делается ночью, по тому есть погрешность.
1 день - 20%
3 день - 30%
5 день - 40%
15 день - 95%
14 дней - 75%
Q - вероятность, N - интересующий день.
Q = 20% + 75% * ((N - 1) / 14)
>за разное количество дней
разницу между двумя результатами вычислиш сам
При N = 3
_____1____14______-20%
Q = 20% + 75% * ((3 - 1)/14) = 30,71428571428571
При N = 5
Q = 20% + 75% * ((5 - 1)/14) = 41,42857142857143
Сверяем с результатом в самом верху.
>>194030
Звонок означает обмен сплетнями между двумя сплетницами. Т.е. если у первой были сплетни А и Б, а у второй В и Г, то после звонка у обоих будут сплетни А, Б, В, Г.
Насчёт времени: не надо усложнять условия, нет там никакого времени, звонок -- моментальное событие.
>>194049
Они звонят наиболее оптимально, т.е. спрашивается, сколько звонков нужно совершить при идеальной стратегии звонков (чем меньше, тем лучше).
>>194055
>А если мы выиграли 0 машин из 0 машин? 0\0 равно Аллах Бабах или все таки 100% выигранных машин?
Деление на ноль - в другом треде.
>>194055
>мы выиграли 0 машин из 0 машин
Такая ситуация просто бессмысленна, зачем её рассматривать? Другая похожая бессмысленная ситуация: выиграна -1 из 0 машин. На вопрос "Сколько процентов выиграно?" ответа быть просто не может.
>>194059
> 15 день - 95%
> 14 дней - 75%
85% и 90%
20% +5% х (14-1) = 85%
> Q = 20% + 75% * ((N - 1) / 14)
1) Делить на 15 надо, не?
2) Максимум не учтен.
3) Не учтена основная проблема. У тебя вероятность работает только если не произойдет событий до дня N.
Наглядный пример:
Вероятность, что за 7 дней событие будет одно и произойдет на третий день:
0.8*0.75*0.3*0.8*0.75*0.7*0.65 = 0.04914
Вероятность, что событие будет одно и произойдет на четвертый день:
0.8*0.75*0.7*0.35*0.8*0.75*0.7 = 0.06174
Подскажите, что почитать по метрическим пространствам. Понятное, доступное.
1 курс мехмата, проебал 3 недели матана, теперь печет.
>>194108
Английскую википедию. Покрывает курс мехмата с лихвой.
>>194107
>1) Делить на 15 надо, не?
Объясни зачем.
>2) Максимум не учтен.
Я далековат от формальности, что ты подразумеваеш?
>3) Не учтена основная проблема. У тебя вероятность работает только если не произойдет событий до дня N.
Если вопрос
>Как рассчитать вероятность какого-то количества событий за разное количество дней (от 5 до 100)?
то ответ:
95/15 = 6,3
6,3*20+6,3*75=598,5%
598,5/95=6,3 события от 5 до 100 дней произойдут с вероятностью 95%.
Поправляй меня.
>>194147
Немного поясню.
получается, что решение Z = Q дней / 15 дней, где Z количество событий, которое произойдёт с вероятностью 95%, а Q = 100 дней (Кончало) - 5 дней (Начало).
>>194147
> Поправляй меня.
У тебя ошибка на генном уровне, имхо.
Почему в Википедии сказано, что математическая индукция -- дедуктивный метод? Ведь на самом деле мы по сути говорим "Для а1 верно, для всех последующих тоже верно, следовательно, для всех а верно", т.е. из утверждений о конкретных элементах множества выводим утверждение для всех элементов множества. В дедукции же наоборот.
(http://ru.wikipedia.org/wiki/%D0%98%D0%BD%D0%B4%D1%83%D0%BA%D1%86%D0%B8%D1%8F_(%D1%84%D0%B8%D0%BB%D0%BE%D1%81%D0%BE%D1%84%D0%B8%D1%8F)#.D0.98.D0.BD.D1.82.D0.B5.D1.80.D0.B5.D1.81.D0.BD.D1.8B.D0.B5_.D1.84.D0.B0.D0.BA.D1.82.D1.8B)
>>194168
Иначе и быть не может. Иные методы вывода, кроме дедуктивного, в формальной математике недопустимы.
Мат. индукция является частным случаем (для счетных множеств) метода трансфинитной индукции. А теорема о трансфинитной индукции доказывается вполне себе дедуктивным путем.
>>194168
Математическая индукция это и есть дедукция.
Если значение равно для n+1 то оно равно для всех следующих значений.
Посоны, возможно моя просьба охуевшая, но можете ли вы мне доступно объяснить, что такое гомология? Доступно, это значит типа: Производная - скорость изменения функции, интеграл - площадь ф-ции под графиком и т.д.
>>194179
Инвариант - то, что сохраняется при преобразованиях. Например, при движениях евклидовой плоскости квадраты переходят в квадраты; посему квадраты - инварианты для перемещений.
Топология изучает непрерывные преобразования. Топологические инварианты - то, что сохраняется при непрерывных взаимно-однозначных преобразованиях (точнее, гомеоморфизмах).
Гомология топологии - это множество всех топологических инвариантов, разбитое на классы эквивалентности.
>>194179
Так, как производную, конечно не получится объяснить. Более общо гомология -- это характеристика пространства, показывающая конфигурацию и число "дырок" разных размерностей.
Это если ты даже не знаешь, что такое группа.
У открытого множества есть граничные точки?
>>194195
Зависит от топологии.
В стандартной топологии на прямой граничными точками (0;5) являются 0 и 5, например.
Ребята, какой алгоритм поиска точек разрыва в функциях от двух переменных?
У меня, например, есть функция u=(xy)/(x+y).
Как мне найти точки разрыва? Прошу, поясните, а дальше я сам.
Я должен доказать, что этот предел существует или не существует в точке y=x=0? Через двойной предел, а дальше по определению, например по Гейне?
>>194197
>В стандартной топологии на прямой граничными точками (0;5) являются 0 и 5, например.
Все остальные точки - внутренние, т.к. окрестность одномерная.
>Зависит от топологии.
Каким образом?
Друзья, поясните за пользу от изучения математики.
Например от 4-5 лет обычной учебы на матфаке.
То есть приходит вчерашний выпускник с способностями к математике выше среднего на матфак, учится, выпускается. По специльности, ясное дело, не работает. Так вот какой профит именно от учебы?
Поумнеет? Станет быстрее строить логические цепочки, видеть на несколько ходов вперед что-то, продумает бизнес-план более детально, чем Васян с экономфака? А?
Серьезно, интересно услышать ответы простым языком, а не вырезки из научных статей о стимулировании мозговых клеток бла бла уменьшается вероятность заболеть какой-нибудь болезнью на 30.76%.
Я не троль, просто сам учусь на матфаке и вот призадумался.
>>194206
>Друзья, поясните за пользу от изучения математики.
Развитие абстрактного мышления, дисциплинирование мышления, способность представления объектов окружающего мира в той или иной математической модели, умение выстраивать доказательство.
>Васян с экономфака
Насколько я знаю в экономике применяется например мат. статистика, методы оптимизаций и регрессионный анализ.
>Я не троль
Хочется верить напрасно.
Почему производная высоких порядков в записи Лейбница записывается, что сверху степень у дифференциала, а снизу у переменной?
>>194872
Хороший вопрос, тоже задумывался, но не придавал значения. Может, потому что оператор d/dx:
(d/dx)(d/dx) = d^2/dx^2
>>194872
Потому что в случае независимой переменной d^2(x)= (dx)^2 , т.е записывать-то можно и со степенью диференциала в знаменателе.
Продублирую вопрос из своего тредика:
Саентаны, кто-нибудь уже проклассифицировал все бесконечные поля конечной характеристики? Какие поля вообще бывают?
Доказать, что множество бесконечно тогда и только тогда, когда существует равномощное ему собственное подмножество.
>>194955
Алгебраические расширения конечный полей. Вполне такое может иметь бесконечное число элемент. (Берем все неприводимые многочлены и строим поле их разложения, например).
Трансцендентные расширения. Т.е. пусть F=K(u1,...,un) - поле частных конечнопорожденного кольца над полем K. Тогда существует базис трансцдентности {v1,...,vk} такой что: L = K(v1,...,vk) - алгебраическое расширение F. (Лемма Нётер о нормализации).
Тогда L - изоморфно полю рациональных функций над полем K от переменными {v1,...,vk}.
Важно, что я тут использовал конечнопорожденность F(То есть, {u1,...,un} - порождают F - значит любой элемент из F представляется в виде линейной комбинации порождающих с коэф. из K.)
Такие дела.
>>195015
> конечных
> элементов
фикс.
Вообще я тут много где наебал и сказал некорректно. Лемма Нётер звучит слегка не так, а про конечнопорожденность - я имел ввиду кольцо, офк, а уже потом по кольцу строил поле частных.
>>195024
А да блять, я лемму Нётер не так сформулировал, там еще условие целости алгебраического расширения, ясен хуй, что взяв любой базис трансцдентности - у нас исходное поле будет алг. расширением.
Каких блять других полей. Вот у тебя есть поле. Определение базиса трансцдентности не зависит от поля. Просто блять какой-то ебанный набор {v1,...,vk}.
Можно наверняка придумать поле в котором не будет конечного базиса трансцдентности. (Ну хуле тут, берем возрастающую цепь таких полей и обхединяем их). Но там наверняка можно обобщить понятие алгебраической зависимости и с помощью трансфинитной индукции и леммы Цорна показать его существование и равномощность всех таких базисов.
Обобщить понятие системы порождающих и показать, что тогда исходное поле - алгебраического(возможно нихуя не конечное) расширения поля, порожденного базисом трансцдентности.
>>195025
В лемме Нётер о нормализации требуется конечная порожденность алгебры. С этим ты, конечно, соснешь. Даже K(t) не конечно порождено над K. Ну, т.е. поле обычно НЕ обладает конечным базисом трансцендентности над другим полем. Что правильно, т.к. вариант теоремы Гильберта о нулях (конечное алгебраическое расширение поля, которое само является полем обязательно должно быть конечным расширением в смысле модулей).
Поэтому неясно у чего ты берешь базис трансцендентности. Нужно искать конечно порожденное кольцо над F_p, полем частных которого является рассматриваемое поле. Почему такое найдется совершенно не очевидно (даже в разумных примерах). Например, алгебраическое замыкание F_p таким не будет (любое конечно порожденное подкольцо будет лежать в каком-то F_(p^n)).
>>195026
Ну ты дурак что ли совсем.
Рассматриваем все множества а.н. систем. Вводим на них предпорядок. Очевидно блять, что оно удоволетворяет лемме Цорна. Значит у нас появляется блядский базис трансцдентности. Легко показывается инвариантность его мощности.
Это, конечно, чудесно, но он будет бесконечный. Что дальше?
>>195027
Это, конечно, чудесно, но он будет бесконечный. Что дальше?
Например, в K(t) у тебя базис будет вида 1/f, где f пробегает некоторое бесконечное подмножество многочленов.
>>195025
Ну в твоих рассуждениях конечность расширяемого поля как-то не особо фигурирует. Так же можно рассуждать и просто про расширения любых полей, но так их все не опишешь же.
>>195027
На самом деле я уже понял, что ты хотел сказать.
Любое поле представляется как алгебраическое расширение (возможно бесконечное) K(x_i). Тогда согласен. И это очевидно.
>>195035
Вот именно. Примеры самые нетривиальные могут быть.
Подскажите, как можно преобразовать следующее выражение: √2cos(4px-p/4) (корень относится только к двойке). Как я понимаю, формулы приведения тут не применить, что с ним тогда можно сделать?
>>195064
Преобразовать можно по-разному, в зависимости от того, что ты дальше с ним хочешь делать. а вообще с такими вопросами тебе скорее в /un/
>>195066 Уточню всё-таки: эта штука вот отсюда - http://alexlarin.net/ege/2014/trvar71.html, задание С1. То есть нужно мне это для решения логарифмического уравнения, и разумеется, способ должен умещаться в рамках школьного курса, такие дела. Кто-нибудь?
>>195069
Косинус разности хуйни, очевидно же. Дальше всё совсем элементарно.
>>195084 я и забыл про существование этой формулы, спасибо
Почему диагональное доказательства Кантора нельзя применить к натуральным числам? Типа, для вещественных доказываем, что найдется такое $x \in \mathbb{R}$, что $(\forall n \in \mathbb{N})(x[n] \neq f(n)[n])$, где $f: \mathbb{N} \leftrightarrow \mathbb{R}$, а $[n]$ обозначает n-й знак после запятой. Следовательно, этому $x$ не может быть поставлено в соотвевтствие никакое натуральное число, а значит множество вещественных числе - несчетно. Почему нельзя спроецировать то же самое на натуральные числа, типа $x \in \mathbb{N}$, а $[n]$ - n-я цифра перед запятой? То есть это $x$ будет отличаться от каждого натурального числа, с которым его сравнивают. Получается чушь, само собой, но что я не учел в доказательстве Кантора?
>>195700
Для тех у кого не стоит плагин для LaTeX
>>195700
Ты доказываешь, что плюс бесконечность не принадлежит множеству натуральных чисел
Понимаешь?
>>195700
Диагональный метод Кантора применим к множеству всех бесконечных последовательностей нулей и единиц, которое не равномощно множеству натуральных чисел, но зато равномощно отрезку [0,1], который, в свою очередь, равномощен R.
>>195702
Да, начинаю понимать. То есть противоречие в том, что $x$ на самом деле не принадлежит множеству натуральных чисел. А в случае с вещественными числами, это $x$ лежит где-то между 0 и 1, а значит это вещественное число и противоречия нет.
>>193579
тут будто сидят школьники неслышавшие что гексанальная структура (соты напр.) – самая экономичная.
Есть рельс и на ней велоколесо, цепь снизу звёздочки тянет её вправо – поедет ли колесо влево? Или что будет?
В виде велосипеда не представляйте – там в этом случае просто рама толкает колесо.
>>195817
Пикрелейтед красную цепь тянут вправо, колесо куда поедет?
>>195878
Зависит от сцепления колеса с поверхностью, может как влево так и вправо.
>>195885
Значит, на сколько я понял, нужны просто достаточный вес и звезда побольше.
Нужна реализация многосеточного геометрического метода. Точнее W-цикл для линейной задачи. Есть у кого?
Ну или просто алгоритм подробный. Помогай, анон.
>>195893
Кстати, надеюсь ни у кого бугурта не вызвал тем, что написал в этом треде т.к треда по примату не нашёл. Мы же всё равно братишки :3
>>187743
0,5 же, хотя если посчитать то да 1. 2кг, ебать лехкотня
Существует ли поле такое, что его мультипликативная группа изоморфна его аддитивной группе?
>>195898
Возьмем (R\{0},*)=G и (R,+) = H.
Мое предположение,что этот пример - ок будет. Ввести структуру Z-модуля, в них нет торсиона, выбрать максимальный идеал в Z и показать, что ранги модулей равны. Приправив все это леммой Цорна.
>>195896
> реализация
А ты не охуел, быдлокодер залётный? Делай домашку сам.
>>195907
/Sci не отличается от /b? Сказал же что алгоритма будет достаточно. Ну или ссылки хотя бы на оный.
>>195902
>Возьмем (R\{0},*)=G и (R,+) = H.
>Мое предположение,что этот пример - ок будет.
Нет. В (R\{0},*) у -1 порядок 2, а в (R,+) все элементы отличные от 0 имеют бесконечный порядок.
>>195925
>/Sci не отличается от /b?
двач – доска уровня /b.
>>187741
Как объяснить быдлу, что девяностые - это промежуток с 1980 по 1989 год. Я это понимаю, но не могу разжевать олигофренам доступно, просто красноречия не хватает. Понятно что быдлу проще ориентироваться так как они привыкли, но всё-таки, есть какой-то способ перевести на язык пещерных людей простые понятные вещи?
>>196025
Уебок, тебе не стремно ссылку на педивикию в научной тематике давать? Я в /б/ над такими мудозвонами насмехаюсь, и членом им по губам провожу.
>>196035
Послал на хуй с википидией, лезет с лурком. По-моему этот даун пытается шутить.
>>196024
Лолчто? Девяностые -- это 1990-е годы (для XX века).
Вообще с годами есть одна проблема, но она заключается только с границей между веками. Вот например: 2000 год относится к XX веку, это не начало XXI века, как когда-то говорили СМИ. Начинается же XXI век ровно тогда, когда начинается 2001 год.
>>187786
3. Вершины ломаной обязаны быть в вершинах куба?
>>190358
В конечномерном случае А=А' (легко строится изоморфизм).
>>191060
Ван дер Ваарден "Алгебра", Ленг "Алгебра" (абстрактно, сцуко).Ну и Кострикин неплох
>>196051
>Сказал "сам такой"
>Сам себя поддвачнул.
Часто тебя дауном называют, а даун?
>>196054
Он не хочет понимать) Внушил себе идею и похуй на всех.
Нормальным людям то очевидно, что 90е – это года девяносто какие-то, как тинейджеры – люди с возрастом заканчивающимся на teen.
>>196261
>Он не хочет понимать)
>)
Еще один даун. Сколько же вас тут. Нормальные люди вообще сидят тут?
>>196024
слыш, пещерный, название "девяностые" не от "девятый десяток", к которому таки относятся 80-89, а от "девяносто-такой-то", просторечие жи.
Ну, насчёт латеха решили?
>>196024
Девяностые - это года с 90 по 99 включая оба. По определению.
Как решить это:
x^2y''-6y=5x^3 + 8x^2.
Нашел решение однородного уравнения. Как теперь неоднородного найти?
>>196024
>но не могу разжевать олигофренам доступно
Следовательно, сам не понимаешь.
Какое понятное и простое определение у гладкого многообразия? Без этих карт и атласов ебучих.
Или объясните, зачем в википедии например рассматриваются какие-то объединения атласов и классы эквивалентности.
>>196333
>Можно говорить как угодно, но понимать надо чуть глубже, чем 2+3.
Зацените пацаны, толстяк оказывается Фромма ботает.
Пример 1.
Есть 2 переменных, которые могут принимать значения от 0 до 255, всего 256.
Чтобы узнать число комбинаций значений этих переменных нужно 256 * 256 = 65536, тут всё понятно.
Пример 2.
Есть две переменных, которые могут принимать значения от 0 до 3 по 3 раза.
Тоесть 3*3 это число комбинаций двух переменных, 3*3*3*3 это число комбинаций комбинаций переменных по 3 раза.
Пример 3.
Есть четыре переменных, которые могут принимать значения от 0 до 3 по 2 раза каждая, при длине комбинации комбинаций равной 5.
Попробую обрисовать.
a = (0;3)
b = a^2
b содержит в себе комбинации двух а
c = b^5
c содержит в себе комбинации пяти b
d = a^2
d содержит в себе комбинации двух d
общее количество комбинаций = b ^ 5 * d, так?
Допустим b = (2;3), которая по счёту это будет комбинация в b? Лопустим b1(2;3);b2(0;3);b3(2;1)b4(1;0)b5(0;0), , которая по счёту это будет комбинация в c?
>>196403
>которая по счёту это будет комбинация в b
Тебе нужно определить правила по которым комбинациям присваиваются номера. Без этого вопрос "какая по счету" бессмысленен.
>>196403
>c = b ^ 5
>b1(2;3);b2(0;3);b3(2;1)b4(1;0)b5(0;0)
фикс
c = b ^ 5 * d
b1(2;3); b2(0;3); b3(2;1); b4(1;0); b5(0;0); d(2;1)
>Тебе нужно определить правила по которым комбинациям присваиваются номера.
Я нихера не понял, но попытаюсь.
Правила такие же как и в системах счисления получается. тоесть увеличение количества цифр в числе = увеличение разрядности числа, цифры в котором могут принимать значения от 0 до 2 (всего три возможных значения).
Пример инкрементации числа из двух разрядов.
00; 01; 02; 10; 11; 12; 20. и т.д., так же изменяется число любой разрядности.
Всё практически тоже самое как и в десятичной системе счисления, просто я выбрал третичную или как её там, дабы цифры были по меньше.
Парни, посоветуйте более современный (и, возможно, качественный) аналог книги Столла "Множества. Логика. Аксиоматические теории". Этакое элементарное введение в основания математики и мат. логику.
>>196465
Есть довольно неплохой учебник Верещагина Шеня.
>>191035
Корень пятой степени из минус единицы. Лдигдействительный две пары комплексносопряженных. Соответственно у тебя будет один x+1 двучлен и два ьрехчлена
>>196335
ищи в виде многочлена третьей степени ax^3 + bx2 + cx + d
Подставляй и приравнивай коэффициерты при степенях x
Посоны, верно ли \sqrt[3]{7-4i} =2(cos(arctg- \frac{7}{7} \times \frac{2}{3} \pi k) + i sin(arctg- \frac{7}{7} \times \frac{2}{3} \pi k)) , k=1, 2 ?
Ох, простите, обосрался. Ладно, без изъёбств пока.
>>196531
>>195701
у меня стоит, но не получается написать, научи, а?
>>195885
$\sqrt[3]{7-4i} =2(cos(arctg- \frac{7}{7} \times \frac{2}{3} \pi k) + i sin(arctg- \frac{7}{7} \times \frac{2}{3} \pi k)) , k=1, 2
\bye ?
>>196533
В формуле поломан скобочный баланс - 3 открывающиеся скобки и 6 закрывающихся.
>>196537
>Равенства нет
Безысходность.
Хуй знает где спрашивать, спрошу здесь.
Препод дал курсач по численным методам, тема - численное интегрирование. Сказал что для метода трапеций есть какое-то (точного названия не помнил) усовершенствование, резко поднимающее точность метода до четвёртой, кажется, но при этом нужно знать вторую производную функции.
Собственно, вопрос в том, что это за метод. Формула Котеса - единственное что я нашёл похожего, но это же просто частный случай формулы трапеций для равномерной сетки, да и вторая производная там только в оценке погрешности.
>>196689
>резко поднимающее порядок точности метода до четвёртой
selffix
Помогите, пожалуйста, новичку.
Не могу понять доказательства.
В случае с пикрелейтед, как я понял, все прямые, по условию, не параллельны ни одной из координатных осей, а значит пересекают координатные оси, следовательно их можно задать уравнением прямой прямой в отрезках на осях, где a - координата пересечения прямой с осью Х, а b - координата пересечения прямой с осью Y.
И как это доказывать по-математически? Что для этого конкретного случая является необходимым и достаточным условиями?
>>196689
Формула Симпсона. Для нее существует оценка погрешности, если интегрируемая функция имеет четвертую производную (см. википедию).
>>196696
Разве недостаточно просто привести каноническое уравнение прямой на плоскости к виду на пикрилейтед? Ограничения формулы будут тогда следовать прямо из канона.
>>196697
Да не, название формулы Симпсона он бы не забыл. Да и там производная четвёртого порядка, а у меня только второго.
>>196703
Из других вариантов, страница http://mathworld.wolfram.com/NumericalIntegration.html привела меня к книге "NUMERICAL RECIPES. The Art of Scientific Computing" (http://goo.gl/oOjI7s ), но и там производные в явном виде требуются только в формуле на странице 167 (second Euler-Maclaurin summation formula).
>>196696
А НЕ ПИЗДИШЬ ЛИ ТЫ ЧАСОМ?
прямая x+y=0 удовлетворяет ограничению на наклон, но что-то не очень-то приводится к виду x/a+y/b=1
>>196891
Ага, в таком виде ведь можно представить только те прямые, в уравнениях которых свободный член ненулевой (т.е. которые не проходят через начало координат).
>>196919
Именно, а значит автор задачи - мудак, и контрится контр-примером.
Уже битый час не могу нагуглить, как решать такие диафантовые уравнения:
229x+188y=1
спасайте!
>>197059
y=(1 - 229*x)*188
>>197070
Поделить на 188 конечно же.
>>197059
А если ты вдруг хотел найти не у, а х, то х=(1-188у)/229.
>>197070
>>197082
Проблема в том, что анону кажется нужны целочисленные решения.
http://ru.wikipedia.org/wiki/Диофантово_уравнение
>>197059
>не может нагуглить, как решать линейные диофантовы уравнения с двумя переменными
А не пиздишь ли ты часом?
чтобы не создавать новый тред спрошу здесь
есть цель поступить в шад или в программерскую магистратуру (сейчас я просто спец, прикладная математика, в универе все проебывал, осел блять) в следующем году, для этого мне надо прокачаться по математике, т.е. по алгебре, матану, теорверу и комбинаторике. как лучше это сделать при сроках в год, анон?
я пока сам придумал следующее:
по алгебре - читаю винберга + делаю задачи из задачника кострикина + с сентября иду слушателем в НМУ
по матану - читаю зорича + задачи
по теор.веру - прохожу курс на edx introduction to probability + читаю какую-нибудь советскую книгу, еще не выбрал какую
по комбинаторике - не знаю пока
и еще думаю надо бы репетитора найти, чтобы.. ну вы понимаете, математикой тяжко одному дома заниматься, надо чтоб кто-то прошаренный направлял и поправлял в случае затупов
как вам план?
А можно почитать про численные методы ( в основном применительно к решению дифуравнений, схемы там всякие итп ) что нибудь концептуальное. Т.е. теорию с выстроенным формализмом, куда все методы стройно укладываются, а не кучу разрозненных глав из учебника.
>>197142
>с сентября иду слушателем в НМУ
Бессмысленная дрочь, если тебе нужны прикладные направления вроде
>шад или в программерскую магистратуру
>репетитора найти
На таком уровне ты никого не найдешь.
>как вам план?
Полное говно. Ты просто корзина, просравшая универ и ищущая способ просрать еще год. Много вас таких по весне оттаивает "я даун, вдруг захотелось стать учоным, посоветуйте какие книги почитать". Доктора Айболита перечитай, дурак.
Бьюсь над задачкой уже несколько часов, как понял она качественная. Анон прошу помогииии...
>>197230
он прав. Я бы посоветовал перечитать незнайку еще.
>>197293
>тред по математике
>задачка по физике
Толсто. Я даже не знаю, что за n и M.
Матаны, я вот считал интеграл, и у меня в ответе получилась вот такая хуйня. Вопрос: квадратный корень из нуля равен нулю, или же у меня несобственный интеграл?
>>197331
Бля, лоханулся. Фикс.
>>197334
Так нет же, всё ок и ты его посчитал, если не обсчитался нигде, конечно, и получил 4/3.
Друже, ты его неправильно посчитал.
Квадратный корень 8 = 2*квадратный корень 2
Пересчитал сейчас на бумажке, сначала нашел неопределенный, потом определенный, путем подставления на место подкорневой хуиты, неизвестную u.
Ты же его как-то по хитрому считаешь.
Пик прилагается.
Кстати, где ты учишься?Если не деанон, конечно же.
>>197350
>На пике, во второй строчке, после du=3x^2 забыл поставить dx
не-быстро-фикс
>>197350
Благодарю. Я удивлён, что интеграл так легко взялся, потому что нашёл его в разделе несобственных интегралов.
Учусь на физфаке ВГУ. А ты где? Интересно, студентам каких вузов посылки из Греции шлют? :-)
>>197379
Там и учусь, Друже, откуда посылки шлют :)
Сейчас готовлюсь сдавать здешний аналог ЕГЭ, там примерно такой уровень сложности, и выше.
По матану комплексные, функции, дифференциалы и интегральчики.
Диффурных уравнений и комплексных функций благо нет, иначе это был бы пиздец.
Общих интегралов(предел в +- бесконечность) тоже нет.
Интересно, короче.
Так что получается ты меня деанонимнул на двощах, о ужас хаха.
Неравнодушен к интегралам, сегодня в 3 ночи увидел твой пост, быром хапнул бомашку и давай решать, даже не заметил что за бумажка.Еще и dx забыл поставить, спросонья.
На каком ты курсе?Что вы учите по матану?По физухе?
>>197386
Я на первом курсе, в школе было тоже самое, что и здесь, но очень поверхностно. А здесь уже были предел, производная, неопределённый интеграл. Сейчас изучаем определённый интеграл. Не могу сказать, что мне всё это сильно нравится, поэтому сюда наведываться буду часто, походу. :-) На физике прошли механику, сейчас долбим МКТ. Всё как в школе, короче, только уровень изложения на голову выше. Удачи на экзаменах. :-)
>>195739
>тут будто сидят школьники неслышавшие что гексанальная структура (соты напр.) – самая экономичная.
тут будто сидят школьники, неслышавшие что "экономичная" требует define, и применяющие общие соображения, которые не могут обосновать.
>>197428
Бурбакист ебонней, пшёл нах)
На какую тему писать курсач по математике?
Не хочется, чтобы все было переписыванием уже известного. Хочется, так сказать, хоть каплю от себя привнести. Может, на прикладную математику обратить внимание?
Помогите младшекуру, господа.
Мои научные интересы лежат где-то среди линейных операторов, алгоритмов. Еще интересно преобразование Фурье.
>>197800-кун
>>196535
что всё это значит? я так и не понял поедет ли колесо при хорошем сцеплении, по моей логике не должно то что тянется вправо ехать влево..
>>197800
Почитай Конкретную математику, рли. Вдохновляющая книга. И что-нибудь из ПРИКЛАДНОЙ МАТЕМАТИКИ там найдёшь.
Могут ли две не параллельные прямые не пересекаться?
из суммы квадратов каких 2х чисел (поменьше бы) можно получить целый корень? ну или хотя бы десятично целый.
>>198171
Друже, а если в пространстве?Не на плоскости а в пространстве, в трех измерениях.
>>198175
В трех измерениях не параллельны и не пересекаются.
Матаны, я думаю, это платина, но есть смысл гуманитарию в 27 лет самому пытаться учить математику? Начать с дифференциального и интегрального исчисления, дифференциальных уравнений, линейной алгебры, а дальше как пойдет. Получу ли я левел-ап к интеллекту/абстрактному мышлению/памяти? И смогу ли за несколько лет, при наличии желания и усидчивости, освоить ваше тайное искусство хотя бы на уровне вузовской программы?
>>198194
Нет, ты отребье, рожденный ползать летать не будет.
Биомусор, пытающийся стать человеком - какая жалость! Особенно забавно смотреть на его надежду, что когда-нибудь он начнет считать себя человеком. Но человеком нельзя становиться, им можно только быть.
>>198194
Учить смысла нет, есть смысл изучать.
>Начать с дифференциального и интегрального исчисления
Лучше со школьной алгебры, евклидовой геометрии и прекалькулуса.
>>198194
>самому пытаться учить
хз, самостоятельная работа требует некоторого уровня адекватности
>хотя бы на уровне вузовской программы?
в вузах как то осиливают, лол. Честно говоря, больше интересно что ты всё это время жрать будешь, если тебе уже 27?
>>198216
что за школьник писал, и масса m и кирпич m? так не считают. и "m=1+1/2m" значит m=1.5m
пиши когда дойдёшь в школе до систем уравнений.
>>198201
>Учить смысла нет, есть смысл изучать.
Ну да, изучать.
>Лучше со школьной алгебры, евклидовой геометрии и прекалькулуса.
Это-то я знаю достаточно уверенно. Мои знания становятся нетвердыми примерно на уровне тригонометрии и производных и заканчиваются на уровне интегралов. Но сейчас работаю сам по "A First Course in Calculus" за авторством Serge Lang (живу не в России, русскоязычные книги достать проблема, разве что с торрентов скачать сканы и распечатать), там прекалькулус разжевывается довольно подробно.
>>198202
>Честно говоря, больше интересно что ты всё это время жрать будешь, если тебе уже 27?
Ну я сейчас пишу диссертацию по политологии. Использую, в том числе, статистику, но, как и большинство коллег-политологов, понимаю ее очень поверхностно - то есть посчитать регрессию в статистической программе могу и распечатку результатов понимаю, но почему это работает - представляю себе очень смутно.
>>198271
>скачать сканы и распечатать
А зачем распечатывать? Скачал и читай с монитора, нахуй таскаться с кипой бумаг.
>>198271
По прекалькулусу как референс рекомендую вот это http://www.stitz-zeager.com/szprecalculus07042013.pdf
>русскоязычные книги достать проблема
Я считаю, англоязычные лучше в большинстве случаев.
>сейчас работаю сам по "A First Course in Calculus" за авторством Serge Lang
Как альтернатива есть "Calculus" от Спивака.
Если хорошо можешь в пруфы, то есть вариант обмазаться вещественным анализом - по двухтомнику Тао, например.
Если с пруфами не очень, попробуй курс https://www.coursera.org/course/maththink.
>>198315
Спасибо, анон!
Про калькулюс от Спивака знаю, даже листал его в библиотеке универа, но Ланга вроде как уже купил, поэтому буду работать по нему.
Особое спасибо за курс на курсере - то, что нужно.
>>198271
Какие нахуй курсеры? Какие нахуй спиваки тао и прочая хуета? Бери учебник алгебры за 10-11 класс и ебашь, ебаный троечник. А когда весь учебник до последнего задания осилишь (т.е. никогда), качай фихтенгольца и ебашь его (ТЕБЕ хватит на пару жизней этого).Всё.
прекалькулус ланг англоязычная литература кококо засрали аспирантуры пустоголовые уебанцы






































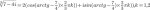



















Тред математики стартует здесь. Задаём свои вопросы, отвечаем на чужие. Две задачки от меня:
1. Кирпич весит килограмм и ещё полкирпича. Сколько весит кирпич?
2. Доказать, что среди любых n+1 чисел из множества {1, 2, ..., 2n} всегда найдутся такие a и b, что a кратно b.